搜索
【题目】把四张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为m，宽为n）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示．则图②中两块阴影部分的周长和是（ ）
A. 4nB. 4mC. 
D. 
参考答案：
【答案】A
【解析】
本题需先设小长方形卡片的长为a，宽为b，再结合图形得出上面的阴影周长和下面的阴影周长，再把它们加起来即可求出答案．
设小长方形卡片的长为a，宽为b，
∴L上面的阴影=2（n-a+m-a），
L下面的阴影=2（m-2b+n-2b），
∴L总的阴影=L上面的阴影+L下面的阴影=2（n-a+m-a）+2（m-2b+n-2b）=4m+4n-4（a+2b），
又∵a+2b=m，
∴4m+4n-4（a+2b），
=4n．
故选：A．
-
科目： 来源： 题型：
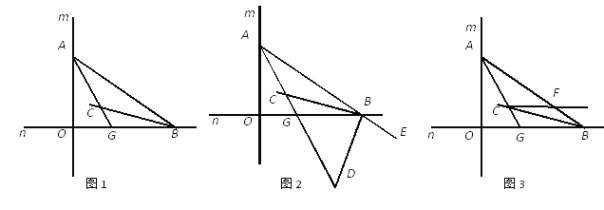
查看答案和解析>>【题目】如图1，直线m与直线n垂直相交于O，点A在直线m上运动，点B 在直线n上运动，AC、BC分别是∠BAO和∠ABO的角平分线．
（1）求∠ACB的大小；
（2）如图2，若BD是△AOB的外角∠OBE的角平分线，BD与AC相交于点D，点A、B在运动的过程中，∠ADB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；
（3）如图3，过C作直线与AB交于F，且满足∠AGO－∠BCF=45°，求证：CF∥OB．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解不等式组
请结合题意，完成本题解答过程．
（1）解不等式①，得 ，依据是 ．
（2）解不等式②，得 ．
（3）解不等式③，得 ．
（4）把不等式①，②和③的解集在数轴上表示出来．
（5）从图中可以找出三个不等式解集的公共部分，得不等式组的解集 ．
（6）根据不等式组的解集确立出该不等式组的最大整数解为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】乘法公式的探究及应用：
数学活动课上,老师准备了若干个如图1的三种纸片，A种纸片边长为
的正方形，B种纸片是边长为
的正方形，C种纸片长为
宽为的长方形，并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形。(1)请用两种不同的方法表示图2大正方形的面积：
方法1:_____________________；方法2:_____________________.
(2)观察图2,请你写出下列三个代数式:
之间的等量关系；(3)类似的,请你用图1中的三种纸片拼一个图形验证:
(4)根据(2)题中的等量关系,解决如下问题:
已知:
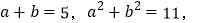求
的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】感知：
如图①，AD平分∠BAC，∠B+∠C＝180°，∠B＝90°．判断DB与DC的大小关系并证明．
探究：
如图②，AD平分∠BAC，∠ABD+∠ACD＝180°，∠ABD＜90°，DB与DC的大小关系变吗？请说明理由．
应用：
如图③，四边形ABDC中，∠B＝45°，∠C＝135°，DB＝DC＝a，则AB﹣AC＝ ．（用含a的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB、BC、AC三边的长分别是
，
，
．（1）△ABC的面积是 ；
（2）请在图1中作出△ABC关于直线l对称的△A1B1C1；
（3）请在图2中画出△DEF，是DE、EF、DF三边的长分别是
，
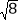，，并判断△DEF的形状，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG交于点H，∠C＝∠EFG，∠CED＝∠GHD．
（1）求证：CE∥GF；
（2）试判断∠AED与∠D之间的数量关系，并说明理由；
（3）若∠EHF＝80°，∠D＝30°，求∠AEM的度数．
相关试题
