【题目】如图,在梯形![]() 中,
中,![]() ,中位线
,中位线![]() 与对角线
与对角线![]() 交于
交于![]() 两点,若
两点,若![]() cm,
cm, ![]() cm,则
cm,则![]() 的长等于( )
的长等于( )

A. 10 cm B. 13 cm C. 20 cm D. 26 cm
参考答案:
【答案】D
【解析】分析:根据梯形的中位线的定理和平行线分线段成比例定理求出AM=CM,NB=DN,然后根据三角形的中位线定理求出CD的长,然后再根据梯形的中位线定理求出AB的长即可.
详解:∵EF是梯形的中位线,
∴EF∥CD∥AB.
∴AM=CM,BN=DN.
∴EM是△ACD的中位线,NF是△BCD的中位线,
∴EM=![]() CD,NF=
CD,NF=![]() CD.
CD.
∴EM=NF=![]() =5,即CD=10.
=5,即CD=10.
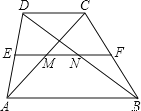
∵EF是梯形ABCD的中位线,
∴DC+AB=2EF,即10+AB=2×18=36.
∴AB=26.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角△ABC中,AD是高,E,F分别是AB,AC中点,EF交AD于G,已知GF=1,AC= 6,△DEG的周长为10,则△ABC的周长为( )

A. 27-3
 B. 28-3
B. 28-3 C. 28-4
C. 28-4 D. 29-5
D. 29-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】以边长为
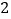 的正方形的中心
的正方形的中心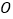 为端点,引两条相互垂直的射线,分别与正方形的边交于
为端点,引两条相互垂直的射线,分别与正方形的边交于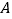 、
、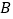 两点,则线段
两点,则线段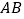 的取值范围是________.
的取值范围是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为
 .
.(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是_________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
,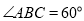 ,
, ,
, 为
为 的中点,若动点
的中点,若动点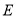 以1
以1 的速度从
的速度从 点出发,沿着
点出发,沿着 的方向运动,设
的方向运动,设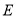 点的运动时间为
点的运动时间为 秒(
秒( ),连接
),连接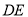 ,当
,当 是直角三角形时,
是直角三角形时, 的值为_____.
的值为_____.
相关试题

