【题目】以边长为![]() 的正方形的中心
的正方形的中心![]() 为端点,引两条相互垂直的射线,分别与正方形的边交于
为端点,引两条相互垂直的射线,分别与正方形的边交于![]() 、
、![]() 两点,则线段
两点,则线段![]() 的取值范围是________.
的取值范围是________.
参考答案:
【答案】![]()
【解析】
先证明△AOE≌△DOF,进而得到OE=OF,此为解决该题的关键性结论;求出OE的范围,借助勾股定理即可解决问题.
如图所示:
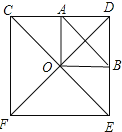
∵四边形CDEF是正方形,
∴∠OCD=∠ODB=45°,∠COD=90°,OC=OD,
∵AO⊥OB,
∴∠AOB=90°,
∴∠COA+∠AOD=90°,∠AOD+∠DOB=90°,
∴∠COA=∠DOB,
在△COA和△DOB中,
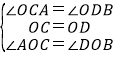 ,
,
∴△COA≌△DOB(ASA),
∴OA=OB,
设OA=OB=a,
∵∠AOB=90°,
∴△AOB是等腰直角三角形,
由勾股定理得:AB2=OA2+OB2=2a2,
由题意可得:1≤a≤![]() ,
,
∴![]() .
.
故答案是:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在
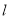 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?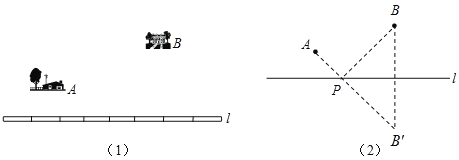
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
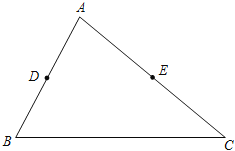
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片
 中,
中,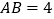 ,
,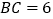 ,将
,将 沿
沿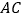 折叠,使点
折叠,使点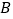 落在点
落在点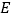 处,
处,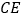 交
交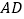 于点
于点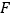 ,则
,则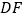 的长等于( )
的长等于( )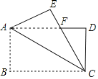
A.
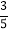 B.
B.  C.
C.  D.
D. 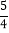
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角△ABC中,AD是高,E,F分别是AB,AC中点,EF交AD于G,已知GF=1,AC= 6,△DEG的周长为10,则△ABC的周长为( )

A. 27-3
 B. 28-3
B. 28-3 C. 28-4
C. 28-4 D. 29-5
D. 29-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为
 .
.(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 中,
中, ,中位线
,中位线 与对角线
与对角线 交于
交于 两点,若
两点,若 cm,
cm,  cm,则
cm,则 的长等于( )
的长等于( )
A. 10 cm B. 13 cm C. 20 cm D. 26 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是_____.

相关试题

