【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,若动点
的中点,若动点![]() 以1
以1![]() 的速度从
的速度从![]() 点出发,沿着
点出发,沿着![]() 的方向运动,设
的方向运动,设![]() 点的运动时间为
点的运动时间为![]() 秒(
秒(![]() ),连接
),连接![]() ,当
,当![]() 是直角三角形时,
是直角三角形时,![]() 的值为_____.
的值为_____.

参考答案:
【答案】2或6或3.5或4.5.
【解析】
先求出AB的长,再分①∠BDE=90°时,DE是ΔABC的中位线,然后求出AE的长度,再分点E在AB上和在BA上两种情况列出方程求解即可;②∠BED=90°时,利用∠ABC的余弦列式求出BE,然后分点E在AB上和在BA上两种情况列出方程求解即可.
解:∵∠ACB=90°,∠ABC=60°,BC=2cm,
∴AB=BC÷![]() =2÷
=2÷![]() =4,
=4,
①∠BDE=90°时,如图(1)
∵D为BC的中点,
∴DE是ΔABC的中位线,
∴AE=![]() AB=
AB=![]() ×4=2,
×4=2,
点E在AB上时,t=2÷1=2秒,
点E在BA上时,点E运动的路程为4×2-2=6,
t=6÷1=6;
②∠BED=90°时,如图(2)
BE=BD![]() =
=![]() ×2×
×2×![]() =
=![]()
点E在AB上时,t=(4-0.5)÷1=3.5,
点E在BA上时,点E运动的路程为4+0.5=4.5,
t=4.5÷1=4.5,
综上所述,t的值为2或6或3.5或4.5.

故答案为:2或6或3.5或4.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC﹣∠COD=∠BOC中,正确的有________(填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,动点E从A出发,沿
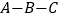 方向运动,当点E到达点C时停止运动,过点E做
方向运动,当点E到达点C时停止运动,过点E做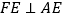 ,交CD于F点,设点E运动路程为x,
,交CD于F点,设点E运动路程为x, 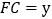 ,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是
,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是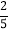 ,则矩形ABCD的面积是( )
,则矩形ABCD的面积是( )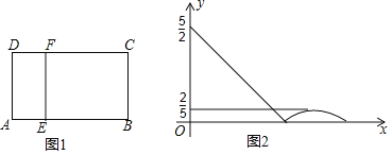
A.
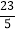 B.
B. 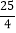 C. 6 D. 5
C. 6 D. 5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,AB=3CD,AB∥CD,CE∥DA,DF∥CB.
(1)求证:四边形CDEF是平行四边形;
(2)填空:
①当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是矩形;
②当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是菱形.
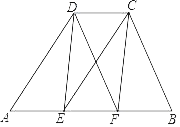
-
科目: 来源: 题型:
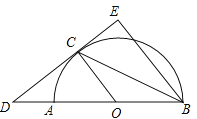
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 是
是 的中点,点
的中点,点 是线段
是线段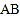 的延长线上的一动点,连接
的延长线上的一动点,连接 ,过点
,过点 作
作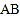 的平行线
的平行线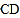 ,与线段
,与线段 的延长线交于点
的延长线交于点 ,连接
,连接 、
、 .
.
 求证:四边形
求证:四边形 是平行四边形.
是平行四边形. 若
若 ,
, ,则在点
,则在点 的运动过程中:
的运动过程中:①当
 ________时,四边形
________时,四边形 是矩形,试说明理由;
是矩形,试说明理由;②当
 ________时,四边形
________时,四边形 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
相关试题

