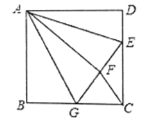
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=CG;③AG//CF;④S△EFC=![]() .其中正确结论的是____________(只填序号).
.其中正确结论的是____________(只填序号).
参考答案:
【答案】①②③④
【解析】
根据正方形的性质得到AB=AD=DC=6,∠B=∠D=90°,求出DE=2,AF=AB,根据HL推出Rt△ABG≌Rt△AFG,推出BG=FG,∠AGB=∠AGF,设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,在Rt△ECG中,由勾股定理得出(6-x)2+42=(x+2)2,求出x=3,得出BG=GF=CG,求出∠AGB=∠FCG,推出AG∥CF,根据![]() ,再求出
,再求出![]() =6,求出S△EFC即可.
=6,求出S△EFC即可.
∵四边形ABCD是正方形,
∴AB=AD=DC=6,∠B=∠D=90°
∵CD=3DE,
∴DE=2,
∵将△ADE沿AE对折至△AFE,
∴DE=EF=2,AD=AF,∠D=∠AFE=∠AFG=90°,
∴Rt△ABG≌Rt△AFG,∴①正确;
∴BG=FG, ∠AGB=∠AGF,
设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,
在Rt△ECG中,由勾股定理得出CG2+CE2=EG2,
即(6-x)2+42=(x+2)2,
求出x=3,
∴BG=GF=CG,②正确;
∵CG=GF,∴∠CFG=∠FCG
∵∠BGF=∠CFG+∠FCG=∠AGB+∠AGF,
∵∠AGB=∠AGF,
∴∠AGB=∠FCG,∴AG∥CF,③正确;
∵![]()
∴S△EFC=![]() ,④正确,
,④正确,
故答案为①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解,并完成填空:在图1至图3中,己知
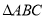 的面积为
的面积为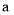 .
.(1)如图1,延长
 C的边
C的边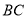 到点
到点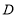 ,使
,使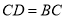 ,连结
,连结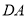 .若
.若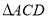 的面积为
的面积为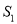 ,则
,则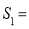 __________(用含
__________(用含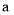 的代数式表示);
的代数式表示);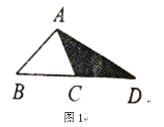
(2)如图2,延长
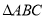 的边
的边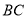 到点
到点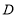 ,延长边
,延长边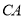 到点
到点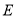 ,使
,使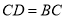 ,
,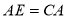 ,连结
,连结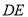 ,若
,若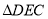 的面积为
的面积为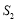 ,则
,则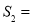 __________(用含
__________(用含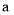 的代数式表示);
的代数式表示);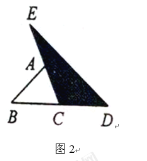
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,得到△DEF(如图3),若阴影部分的面积为S3,则S3=___(用含a的代数式表示)。
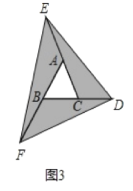
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点
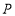 以每秒
以每秒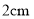 的速度沿如图甲所示的边框按从
的速度沿如图甲所示的边框按从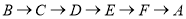 的路径匀速移动,相应的
的路径匀速移动,相应的 的面积
的面积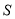 关于时间
关于时间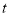 的图象如图乙所示,若
的图象如图乙所示,若 ,试回答下列问题:
,试回答下列问题: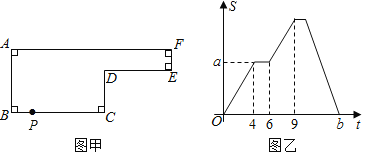
(1)求出图甲中
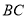 的长和多边形
的长和多边形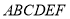 的面积;
的面积;(2)直接写出图乙中
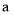 和
和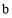 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O……依此规律,得到等腰直角三角形A2 017OB2 017.则点B2 017的坐标( )

A. (22 017,-22 017) B. (22 016,-22 016) C. (22 017,22 017) D. (22 016,22 016)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
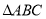 中,已知
中,已知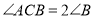 ,
,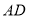 为
为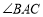 的角平分线.\
的角平分线.\(1)如图1,当
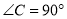 时,在
时,在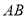 边上截取
边上截取 ,连接
,连接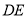 ,你能发现线段
,你能发现线段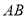 、
、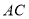 、
、 之间有怎样的数量关系么?请直接写出你的发现:________________________(不需要证明);
之间有怎样的数量关系么?请直接写出你的发现:________________________(不需要证明);
(2)如图2,当
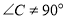 时,线段
时,线段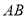 、
、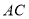 、
、 还有(1)中的数量关系么?请证明你的猜想;
还有(1)中的数量关系么?请证明你的猜想;(3)如图3,当
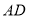 为
为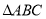 的外角平分线时,线段
的外角平分线时,线段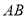 、
、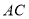 、
、 又有怎样的数量关系?不需要证明,请直接写出你的猜想:______________________.
又有怎样的数量关系?不需要证明,请直接写出你的猜想:______________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得7条折痕,那么对折四次可以得到 条折痕,如果对折
 次,可以得到 条折痕.
次,可以得到 条折痕.
相关试题

