【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
参考答案:
【答案】数量关系为:BE=EC,位置关系是:BE⊥EC.
证明:∵△AED是直角三角形,∠AED=90°,且有一个锐角是45°,
∴∠EAD=∠EDA=45°,
∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=90°+45°=135°,
∠EDC=∠ADC-∠EDA=180°-45°=135°,
∴∠EAB=∠EDC,
∵D是AC的中点,
∴AD= ![]() AB,
AB,
∵AC=2AB,
∴AB=DC,
∴△EAB≌△EDC,
∴EB=EC,且∠AEB=∠AED=90°,
∴∠DEC+∠BED=∠AED=∠BED=90°,
∴BE⊥ED.
【解析】略
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于点M,N,给出下列结论:①△ABM≌△CDN;②AM=
 AC;③DN=2NF;④S△AMB=
AC;③DN=2NF;④S△AMB= S△ABC,其中正确的结论是__ __.(填序号)
S△ABC,其中正确的结论是__ __.(填序号)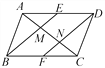
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的表达式;
(2)求直线BC的表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在利用正六面体骰子进行频率估计概率的实验中,小闽同学统计了某一结果朝上的频率,绘出的统计图如图所示,则符合图中情况的可能是( )
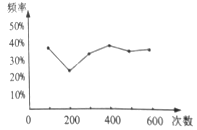
A. 朝上的点数是6的概率B. 朝上的点数是偶数的概率
C. 朝上的点数是小于4的概率D. 朝上的点数是3的倍数的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AE是ΔABC的角平分线,AD是BC边上的高。若∠ABC=34°,∠ACB=64°,则∠DAE的大小是( )
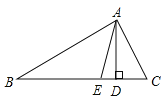
A. 5°B. 13°C. 15°D. 20°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,他手中持有的钱数(含备用零钱)y与售出的土豆千克数x的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是______元,降价前他每千克土豆出售的价格是______元;
(2)降价后他按每千克0.8元将剩余土豆售完,这时他手中的钱(含备用零钱)是62元,求降价后的线段所表示的函数表达式并写出它的取值范围.
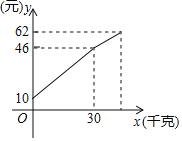
-
科目: 来源: 题型:
查看答案和解析>>【题目】将大小不同的两个正方形按图1,图2的方式摆放.若图1中阴影部分的面积是6,图2中阴影部分的面积是5,则大正方形的面积是________.

相关试题

