【题目】如图①,平面直角坐标系XOY中,若A(0,a)、B(b,0)且(a﹣4)2+![]() =0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
=0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
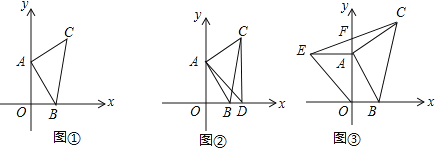
(1)求C点坐标;
(2)如图②过C点作CD⊥X轴于D,连接AD,求∠ADC的度数;
(3)如图③在(1)中,点A在Y轴上运动,以OA为直角边作等腰Rt△OAE,连接EC,交Y轴于F,试问A点在运动过程中S△AOB:S△AEF的值是否会发生变化?如果没有变化,请直接写出它们的比值 (不需要解答过程或说明理由).
参考答案:
【答案】(1)C点坐标为(4,5);(2)∠ADC=45°;(3)2.
【解析】试题分析:(1)作CM⊥OA于M,由非负性质求出a=4,b=1,由AAS证明△CAM≌△ABO,得出MC=OA=4,MA=OB=1,求出OM=OA+MA=5,即可得出C点坐标;
(2)证出OD=OA,得出△OAD为等腰直角三角形,得出∠ADO=45°,求出∠ADC=45°即可;
(3)先判断出△AEF≌△MCF,进而求出AM,最后用三角形的面积公式即可得出结论;
试题解析:(1)作CM⊥OA于M,如图①所示:
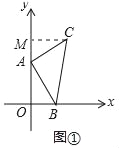
则∠CMA=∠AOB=90°,
∴∠OAB+∠ABO=90°,
∵(a﹣4)2+![]() =0,
=0,
∴a﹣4=0,b﹣1=0,
∴a=4,b=1,
∴OA=4,OB=1,
∵∠CAB=90°,
∴∠OAB+∠CAM=90°,
∴∠CAM=∠ABO,
在△CAM和△ABO中,
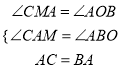 ,
,
∴△CAM≌△ABO(AAS),
∴MC=OA=4,MA=OB=1,
∴OM=OA+MA=5,
∴C点坐标为(4,5);
(2)∵CD⊥x轴,∴D(4,0),
∴OD=OA,
∴△OAD为等腰直角三角形,
∴∠ADO=45°,
∴∠ADC=90°﹣45°=45°;
(3)A点在运动过程中S△AOB:S△AEF的值不会发生变化,S△AOB:S△AEF=2;
理由如下:作CM⊥OA于M,如图③所示:
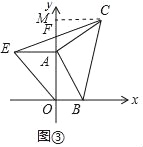
由(1)知,A(0,4),C(4,5),
∴OA=CM=4,
∵△AEO是等腰直角三角形,
∴AE=OA=4,∠OAE=90°,
∴∠EAF=∠OAE=90°=∠CMF,
∵∠AFE=∠MFC,AE=CM,
∴△AEF≌△MCF,
∴AF=MF=![]() AM,
AM,
∵C(4,5),A(0,4),
∴AM=1,
∴MF=![]() ,
,
∴S△AEF=S△MCF=![]() MF×CM=
MF×CM=![]() ×
×![]() ×4=1,
×4=1,
S△AOB=![]() OA×OB=
OA×OB=![]() ×4×1=2,
×4×1=2,
∴S△AOB:S△AEF=2:1=2,
即S△AOB:S△AEF的值是定值,不会发生变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知AD∥BC,∠B=∠D=120°.
(1)请问:AB与CD平行吗?为什么?
(2)若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.
(3)若点E在直线CD上,且满足∠EAC=
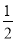 ∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).
∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).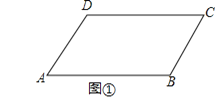

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图正比例函数y=k1x与反比例函数
 交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4.
交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4.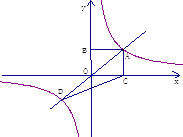
(1)分别求出正比例函数与反比例函数的解析式;
(2)求出正、反比例函数图象的另外一个交点坐标。
(3)求△ODC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(1)请你画出将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1;
(2)线段OA1的长度是______,∠AOB1的度数是______;
(3)连接AA1,求证:四边形OAA1B1是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了预防流感,某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)x4·x6-(x5)2;
(2)(-xy)2·x4y+(-2x2y)3;
(3)(1-3a)2-2(1-3a);
(4)(a+2b)(a-2b)-
 b(a-8b).
b(a-8b). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
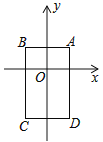
A. (﹣1,﹣2) B. (―1,1)
C. (-1,-1) D. (1,―2)
相关试题

