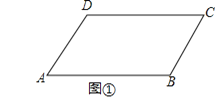
【题目】如图①,已知AD∥BC,∠B=∠D=120°.
(1)请问:AB与CD平行吗?为什么?
(2)若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.
(3)若点E在直线CD上,且满足∠EAC=![]() ∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).
∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).

参考答案:
【答案】(1)平行,理由见解析;(2)∠FAC =30°;(3)∠ACD:∠AED=2:3或2:1.
【解析】试题分析:(1)依据平行线的性质以及判定,即可得到AB∥CD;
(2)依据AC平分∠BAE,AF平分∠DAE,即可得到∠EAC=![]() ∠BAE,∠EAF=
∠BAE,∠EAF=![]() ∠DAE,进而得出∠FAC=∠EAC+∠EAF=
∠DAE,进而得出∠FAC=∠EAC+∠EAF=![]() (∠BAE+∠DAE)=
(∠BAE+∠DAE)=![]() ∠DAB;
∠DAB;
(3)分两种情况讨论:当点E在线段CD上时;当点E在DC的延长线上时,分别依据AB∥CD,进而得到∠ACD:∠AED的值.
试题解析:解:(1)平行.
如图①.∵AD∥BC,∴∠A+∠B=180°.
又∵∠B=∠D=120°,∴∠D+∠A=180°,∴AB∥CD;
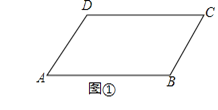
(2)如图②.∵AD∥BC,∠B=∠D=120°,∴∠DAB=60°.
∵AC平分∠BAE,AF平分∠DAE,∴∠EAC=![]() ∠BAE,∠EAF=
∠BAE,∠EAF=![]() ∠DAE,
∠DAE,
∴∠FAC=∠EAC+∠EAF=![]() (∠BAE+∠DAE)=
(∠BAE+∠DAE)=![]() ∠DAB=30°;
∠DAB=30°;
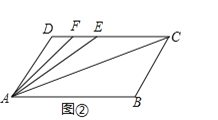
(3)①如图3,当点E在线段CD上时,
由(1)可得AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE.
又∵∠EAC=![]() ∠BAC,∴∠ACD:∠AED=2:3;
∠BAC,∴∠ACD:∠AED=2:3;
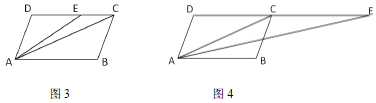
②如图4,当点E在DC的延长线上时,
由(1)可得AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE.
又∵∠EAC=![]() ∠BAC,∴∠ACD:∠AED=2:1.
∠BAC,∴∠ACD:∠AED=2:1.
综上所述:∠ACD:∠AED=2:3或2:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读教科书情况统计图表
类别
人数
占总人数比例
重视
a
b
一般
57
0.285
不重视
c
0.36
说不清楚
9
0.045
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2500名,请估计该校“重视阅读教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读教科书的现状的看法及建议;
②如果要了解全省初中生阅读教科书的情况,你认为应该如何进行抽样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.

①请你根据图象提供的信息求出此蓄水池的蓄水量;
②写出此函数的解析式;
③若要6h排完水池中的水,那么每小时的排水量应该是多少?
④如果每小时排水量是5m3,那么水池中的水将要多少小时排完?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,∠1=∠2,要使△ABC≌△ADE,还需添加的条件是_________.(只需填一个)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图正比例函数y=k1x与反比例函数
 交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4.
交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4.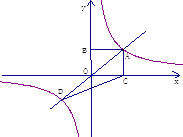
(1)分别求出正比例函数与反比例函数的解析式;
(2)求出正、反比例函数图象的另外一个交点坐标。
(3)求△ODC的面积.
-
科目: 来源: 题型:
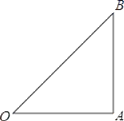
查看答案和解析>>【题目】如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(1)请你画出将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1;
(2)线段OA1的长度是______,∠AOB1的度数是______;
(3)连接AA1,求证:四边形OAA1B1是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,平面直角坐标系XOY中,若A(0,a)、B(b,0)且(a﹣4)2+
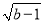 =0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
=0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.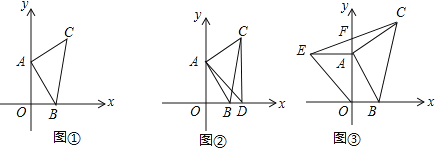
(1)求C点坐标;
(2)如图②过C点作CD⊥X轴于D,连接AD,求∠ADC的度数;
(3)如图③在(1)中,点A在Y轴上运动,以OA为直角边作等腰Rt△OAE,连接EC,交Y轴于F,试问A点在运动过程中S△AOB:S△AEF的值是否会发生变化?如果没有变化,请直接写出它们的比值 (不需要解答过程或说明理由).
相关试题

