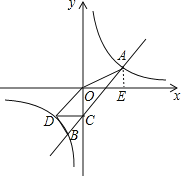
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A、B两点,点A坐标为
的图象交于A、B两点,点A坐标为![]() ,点B坐标为
,点B坐标为![]() ,OA与x轴正半轴夹角的正切值为
,OA与x轴正半轴夹角的正切值为![]() ,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
(1)求一次函数与反比例函数的解析式;
(2)连接BD,求出BDC的周长.

参考答案:
【答案】(1)y=x-2, ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据正切值,可得OE的长,可得A点坐标,根据待定系数法,可得反比例函数解析式,根据点的坐标满足函数解析式,可得B点坐标,根据待定系数法,可得一次函数解析式;
(2)根据坐标系内两点间的距离公式分别求出CD、BD、BC的长,即可得出△BDC的周长.
试题解析:
解:(1)如图:过A做AE⊥x轴于E,
∵tan∠AOE=![]() =
=![]() =
=![]() ,
,
∴OE=4,
∴A(4,2),
∵y=![]() 的图象过A(4,2),
的图象过A(4,2),
∴2=![]() ,
,
解得k=8,
∴反比例函数的解析式为 y=![]() ,
,
B(-2,n)在 y=![]() 的图象上,
的图象上,
解得n=-4,
∴B(-2,-4),
一次函数y=kx+b过A、B点,
∴![]() ,
,
解得![]() ,
,
一次函数解析式为y=x-2;
(2)当x=0时,y=-2,
∴C(0,-2),
当y=-2时,-2=![]() ,
,
x=-4,
∴D(-4,-2),
∴CD=4,BD=![]() =
=![]() ,
,
BC=![]() =
=![]() ,
,
∴△BDC的周长=![]() +
+![]() +4
+4
=![]() +4.
+4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:我们把
 称为二阶行列式,规定它的运算法则为
称为二阶行列式,规定它的运算法则为 =ad﹣bc,例如:
=ad﹣bc,例如: =2×5﹣3×4=﹣2.
=2×5﹣3×4=﹣2.(1)填空:若
 =0,则x= ,
=0,则x= , >0,则x的取值范围 ;
>0,则x的取值范围 ;(2)若对于正整数m,n满足,1
 <3,求m+n的值;
<3,求m+n的值;(3)若对于两个非负数x,y,
 =
=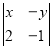 =k﹣1,求实数k的取值范围.
=k﹣1,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD⊥AC,AB=8,AC=
 ,∠A=30°.
,∠A=30°.(1)请求出线段AD的长度;
(2)请求出sin∠C的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
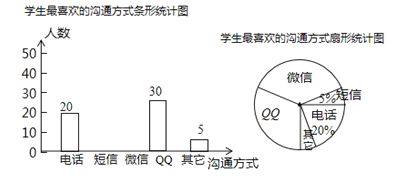
(1)这次统计共抽查了________名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为___________;
(2)请将条形统计图补充完整;
(3)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着网络的发展,我们的生活越来越方便,越来越多的人在网络上购物,微商这个行业也悄然兴起,很多人通过微信平台销售商品.
(1)某水果微商今年九月购进榴莲和奇异果共1000千克,它们的进价均为每千克24 元,然后以榴莲售价每千克45元,奇异果售价每千克36元的价格很快销售完,若该水果微商九月获利不低于17400元,求应购进榴莲至少多少千克?
(2)为了增加销售量,获得更大的利润,在进价不变的情况下,该水果微商十月决定调整售价,榴莲的售价在九月的基础上下调
 (降价后的售价不低于进价),奇异果的售价在九月的基础上上涨
(降价后的售价不低于进价),奇异果的售价在九月的基础上上涨 ,同时,与(1)中获得的最低利润时的销售量相比,榴莲的销售量下降了
,同时,与(1)中获得的最低利润时的销售量相比,榴莲的销售量下降了 ,而奇异果的销售量上升了
,而奇异果的销售量上升了 ,结果十月的销售额比九月增加了600元.求
,结果十月的销售额比九月增加了600元.求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(a,0),B(b,3),C(4,0),且满足
 +(a﹣b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.
+(a﹣b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.(1)求出点A,B的坐标;
(2)如图2,若DB∥AC,∠BAC=a,且AM,DM分别平分∠CAB,∠ODB,求∠AMD的度数;(用含a的代数式表示).
(3)如图3,坐标轴上是否存在一点P,使得△ABP的面积和△ABC的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

相关试题

