【题目】[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为(![]() ,
,![]() ).
).
[运用]
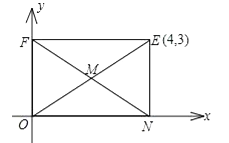
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
参考答案:
【答案】M(2,1.5);(2)D(1,﹣1)或D(﹣3,5)或D(5,3).
【解析】试题分析:(1)先根据四边形ONEF是矩形,所以矩形的性质可以知道点M是对角线OE的中点,根据题中给出的线段的中点坐标公式即可得出M点的坐标;
(2)根据题意画出图形,然后分三种情况:①当AB为对角线时, ②当BC为对角线时, ③当AC为对角线时,求出点D的坐标.
解:(1)![]() 四边形ONEF是矩形,且
四边形ONEF是矩形,且![]() ,
,
![]() 点M是对角线OE的中点,
点M是对角线OE的中点,
![]() ,即
,即![]() .
.
因此,本题正确答案是:![]() ;
;
(2)如图所示:
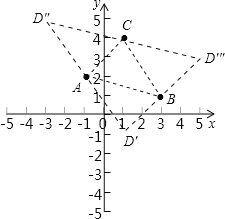
根据平行四边形的对角线互相平分可得:
设D点的坐标为![]() ,
,
![]() 以点A、B、C、D构成的四边形是平行四边形,
以点A、B、C、D构成的四边形是平行四边形,
①当AB为对角线时,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,
②当BC为对角线时,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
D点坐标为![]() .
.
③当AC为对角线时,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
D点坐标为:![]() ,
,
综上所述,符合要求的点有:![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=5,cos∠ABC=
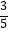 ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;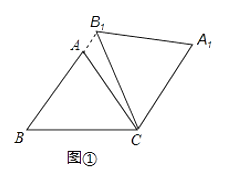
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.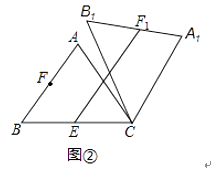
-
科目: 来源: 题型:
查看答案和解析>>【题目】一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为
 ,剩下的水量为
,剩下的水量为 .下面能反映
.下面能反映 与
与 之间的关系的大致图象是( )
之间的关系的大致图象是( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列推理过程:如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD 的度数.
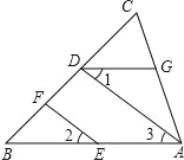
∵ EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)
∴∠1=∠3(等量代换)
∴ AB∥ ( )
∴∠BAC+ =180°(两直线平行 ,同旁内角互补)
∵∠BAC=80°(已知)
∴∠AGD=
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a=﹣ .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;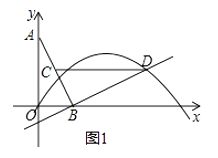
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是4个,请直接写出a的取值范围.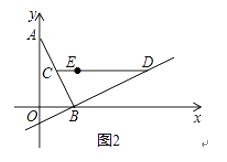
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了了解九年级女生仰卧起坐训练情况,课外活动时间随机抽取10名女生测试,成绩如下表所示,那么这10名女生测试成绩的众数与中位数依次是( )
女生编号
1
2
3
4
5
6
7
8
9
10
成绩/个
48
49
52
47
51
53
52
49
51
49
A.52,51
B.51,51
C.49,49
D.49,50 -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式
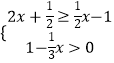 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.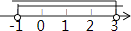
B.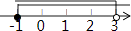
C.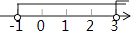
D.
相关试题

