【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a=﹣ ![]() .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;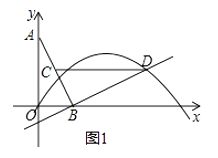
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是4个,请直接写出a的取值范围.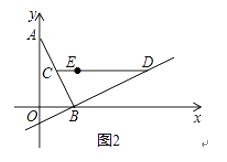
参考答案:
【答案】
(1)解:①过点D作DF⊥x轴于点F,如图1,
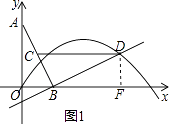
∵∠DBF+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠DBF=∠BAO,
又∵∠AOB=∠BFD=90°,AB=BD,
在△AOB和△BFD中,
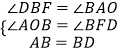 ,
,
∴△AOB≌△BFD(AAS)
∴DF=BO=1,BF=AO=2,
∴D的坐标是(3,1),
根据题意,得a=﹣ ![]() ,c=0,且a×32+b×3+c=1,
,c=0,且a×32+b×3+c=1,
∴b= ![]() ,
,
∴该抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x;
x;
②∵点A(0,2),B(1,0),点C为线段AB的中点,
∴C( ![]() ,1),
,1),
∵C、D两点的纵坐标都为1,
∴CD∥x轴,
∴∠BCD=∠ABO,
∴∠BAO与∠BCD互余,
要使得∠POB与∠BCD互余,则必须∠POB=∠BAO,
设P的坐标为(x,﹣ ![]() x2+
x2+ ![]() x),
x),
(Ⅰ)当P在x轴的上方时,过P作PG⊥x轴于点G,如图2,
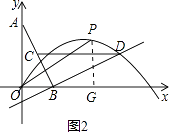
则tan∠POB=tan∠BAO,即 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得x1=0(舍去),x2=
,解得x1=0(舍去),x2= ![]() ,
,
∴﹣ ![]() x2+
x2+ ![]() x=
x= ![]() ,
,
∴P点的坐标为( ![]() ,
, ![]() );
);
(Ⅱ)当P在x轴的下方时,过P作PG⊥x轴于点G,如图3
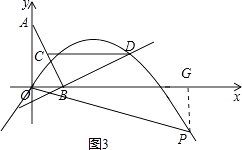
则tan∠POB=tan∠BAO,即 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得x1=0(舍去),x2=
,解得x1=0(舍去),x2= ![]() ,
,
∴﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() ,
,
∴P点的坐标为( ![]() ,﹣
,﹣ ![]() );
);
综上,在抛物线上是否存在点P( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() ),使得∠POB与∠BCD互余
),使得∠POB与∠BCD互余
(2)解:如图3,
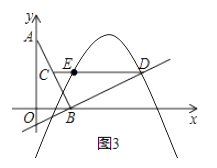
∵D(3,1),E(1,1),
抛物线y=ax2+bx+c过点E、D,代入可得 ![]() ,解得
,解得 ![]() ,所以y=ax2﹣4ax+3a+1.
,所以y=ax2﹣4ax+3a+1.
分两种情况:
①当抛物线y=ax2+bx+c开口向下时,若满足∠QOB与∠BCD互余且符合条件的Q点的个数是4个,则点Q在x轴的上、下方各有两个.
(i)当点Q在x轴的下方时,直线OQ与抛物线有两个交点,满足条件的Q有2个;
(ii)当点Q在x轴的上方时,要使直线OQ与抛物线y=ax2+bx+c有两个交点,抛物线y=ax2+bx+c与x轴的交点必须在x轴的正半轴上,与y轴的交点在y轴的负半轴,所以3a+1<0,解得a<﹣ ![]() ;
;
②当抛物线y=ax2+bx+c开口向上时,点Q在x轴的上、下方各有两个,
(i)当点Q在x轴的上方时,直线OQ与抛物线y=ax2+bx+c有两个交点,符合条件的点Q有两个;
(ii)当点Q在x轴的下方时,要使直线OQ与抛物线y=ax2+bx+c有两个交点,符合条件的点Q才两个.
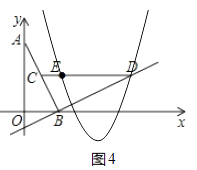
根据(2)可知,要使得∠QOB与∠BCD互余,则必须∠QOB=∠BAO,
∴tan∠QOB=tan∠BAO= ![]() =
= ![]() ,此时直线OQ的斜率为﹣
,此时直线OQ的斜率为﹣ ![]() ,则直线OQ的解析式为y=﹣
,则直线OQ的解析式为y=﹣ ![]() x,要使直线OQ与抛物线y=ax2+bx+c有两个交点,所以方程ax2﹣4ax+3a+1=﹣
x,要使直线OQ与抛物线y=ax2+bx+c有两个交点,所以方程ax2﹣4ax+3a+1=﹣ ![]() x有两个不相等的实数根,所以△=(﹣4a+
x有两个不相等的实数根,所以△=(﹣4a+ ![]() )2﹣4a(3a+1)>0,即4a2﹣8a+
)2﹣4a(3a+1)>0,即4a2﹣8a+ ![]() >0,解得a>
>0,解得a> ![]() (a<
(a< ![]() 舍去)
舍去)
综上所示,a的取值范围为a<﹣ ![]() 或a>
或a> ![]() .
.
【解析】(1)①过点D作DF⊥x轴于点F,先依据AAS证明△AOB≌△BFD,从而可得到D的坐标,然后将点D的坐标代入到抛物线的解析式求解即可;②先证得CD∥x轴,故此可得到∠POB=∠BAO,设P的坐标为(x,-![]() x2+
x2+![]() x),分为P在x轴的上方,P在x轴的下方两种情况画出图形,过P作PG⊥x轴于点G,然后依据锐角三角函数的定义列比例式求解即可;
x),分为P在x轴的上方,P在x轴的下方两种情况画出图形,过P作PG⊥x轴于点G,然后依据锐角三角函数的定义列比例式求解即可;
(2)如果使得符合条件的Q点的个数是4个,那么当a<0时,抛物线交于y轴的负半轴,当a>0时,最小值得<-1,接下来,解关于a的不等式即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为
 ,剩下的水量为
,剩下的水量为 .下面能反映
.下面能反映 与
与 之间的关系的大致图象是( )
之间的关系的大致图象是( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列推理过程:如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD 的度数.
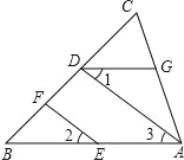
∵ EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)
∴∠1=∠3(等量代换)
∴ AB∥ ( )
∴∠BAC+ =180°(两直线平行 ,同旁内角互补)
∵∠BAC=80°(已知)
∴∠AGD=
-
科目: 来源: 题型:
查看答案和解析>>【题目】[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为(
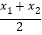 ,
,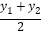 ).
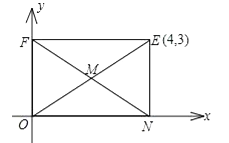
).[运用]
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了了解九年级女生仰卧起坐训练情况,课外活动时间随机抽取10名女生测试,成绩如下表所示,那么这10名女生测试成绩的众数与中位数依次是( )
女生编号
1
2
3
4
5
6
7
8
9
10
成绩/个
48
49
52
47
51
53
52
49
51
49
A.52,51
B.51,51
C.49,49
D.49,50 -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式
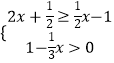 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.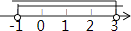
B.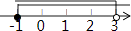
C.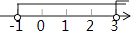
D.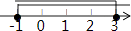
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数记为x,计算|x﹣3|,则其结果恰为1的概率是( )
A.
B.
C.
D.
相关试题

