【题目】在△ABC中,AB=AC=5,cos∠ABC= ![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;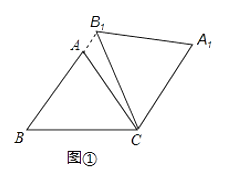
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.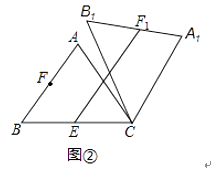
参考答案:
【答案】
(1)解:①证明:∵AB=AC,B1C=BC,
∴∠AB1C=∠B,∠B=∠ACB,
∵∠AB1C=∠ACB(旋转角相等),
∴∠B1CA1=∠AB1C,
∴BB1∥CA1;
②过A作AF⊥BC于F,过C作CE⊥AB于E,如图①:
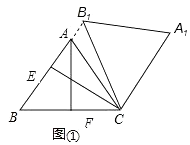
∵AB=AC,AF⊥BC,
∴BF=CF,
∵cos∠ABC= ![]() ,AB=5,
,AB=5,
∴BF=3,
∴BC=6,
∴B1C=BC=6,
∵CE⊥AB,
∴BE=B1E= ![]() ,
,
∴BB1= ![]() ,CE=
,CE= ![]() ,
,
∴AB1= ![]() ,
,
∴△AB1C的面积为: ![]()
(2)解:如图2,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值,
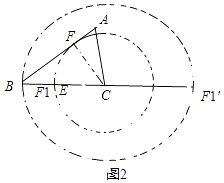
此时在Rt△BFC中,CF= ![]() ,
,
∴CF1= ![]() ,
,
∴EF1的最小值为 ![]() ;
;
如图,以C为圆心BC为半径画圆交BC的延长线于F1,EF1有最大值;
此时EF1=EC+CF1=3+6=9,
∴线段EF1的最大值与最小值的差为 ![]()
【解析】(1)①先依据等腰三角形的性质和旋转的性质可证明∠B1CA1=∠AB1C,最后,再依据平行线的性质进行证明即可;②过A作AF⊥BC于F,过C作CE⊥AB于E,根据三角函数的定义和三角形的面积公式进行计算即可;
(2)过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,以C为圆心BC为半径画圆交BC的延长线于F1,依据图形可得到EF取得最大值和最小值的条件,最后,再求得两条线段的差即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车.经市场调查得知,购买6辆男式单车与8辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16 000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单车比女式单车多5辆,两种单车至少需要22辆,购置两种单车的费用不超过50 000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC和△DEF中,将△DEF按要求摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,若∠A=50°,∠E+∠F=100°,则∠D= ;∠ABD+∠ACD= .
(2)当将△DEF如图2摆放时,∠A=m°,∠E+∠F=n°,请求出∠ABD+∠ACD的度数(用含m、n的代数式表示).
(3)能否将△DEF摆放到某个位置,使得BD、CD同时平分∠ABC和∠ACB.若能,求出∠A、∠E、∠F满足的关系?若不能,请说明理由?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度 y(cm)与所挂物体的质量 x(kg)之间有如下表关系:

下列说法不正确的是( )
A.y 随 x 的增大而增大B.所挂物体质量每增加 1kg弹簧长度增加 0.5cm
C.所挂物体为 7kg时,弹簧长度为 13.5cmD.不挂重物时弹簧的长度为 0cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为
 ,剩下的水量为
,剩下的水量为 .下面能反映
.下面能反映 与
与 之间的关系的大致图象是( )
之间的关系的大致图象是( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列推理过程:如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD 的度数.
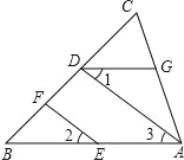
∵ EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)
∴∠1=∠3(等量代换)
∴ AB∥ ( )
∴∠BAC+ =180°(两直线平行 ,同旁内角互补)
∵∠BAC=80°(已知)
∴∠AGD=
-
科目: 来源: 题型:
查看答案和解析>>【题目】[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为(
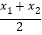 ,
,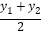 ).
).[运用]
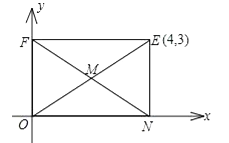
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
相关试题

