【题目】在平面直角坐标系中,O为原点,点A(﹣![]() ,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
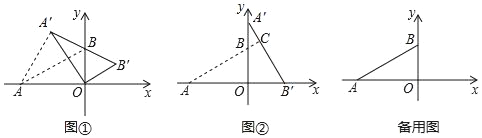
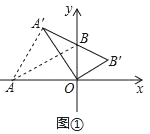
(1)如图①,当点A′,B,B′共线时,求AA′的长.
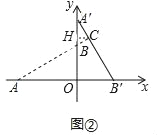
(2)如图②,当α=90°,求直线AB与A′B′的交点C的坐标;
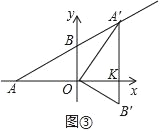
(3)当点A′在直线AB上时,求BB′与OA′的交点D的坐标(直接写出结果即可)
参考答案:
【答案】(1)AA′=![]() ;(2)(
;(2)(![]() ,
,![]() );(3)(
);(3)(![]() ,
,![]() ).
).
【解析】
(1)如图①,只要证明△AOA′是等边三角形即可;
(2)如图②,当α=90°,点A′在y轴上,作CH⊥OA′于H.解直角三角形求出BH,CH即可解决问题;
(3)如图③,设A′B′交x轴于点K.首先证明A′B′⊥x轴,求出OK,A′K即可解决问题;
(1)如图①,
∵A(﹣![]() ,0),B(0,1),
,0),B(0,1),
∴OA=![]() ,OB=1,
,OB=1,
∴tan∠BAO=![]() ,
,
∴∠BAO=30°,∠ABO=60°,
∵△A′OB′是由△AOB旋转得到,
∴∠B′=∠ABO=60°,OB=OB′,OA=OA′,
∴∠OBB′=60°,
∴∠BOB′=α=∠AOA′=60°,
∴△AOA′是等边三角形,
∴AA′=OA=![]() .
.
(2)如图②,当α=90°,点A′在y轴上,作CH⊥OA′于H.
∵∠A′B′O=60°,∠CAB′=30°,
∴∠ACB′=90°,
∵A′B=OA′﹣OB=![]() ﹣1,∠BA′C=30°,
﹣1,∠BA′C=30°,
∴BC=![]() A′B=
A′B=![]() ,
,
∵∠HBC=60°,
∴BH=![]() BC=
BC=![]() ,CH=
,CH=![]() BH=
BH=![]() ,
,
∴OH=1+BH=![]() ,
,
∴点C的坐标(![]() ,
,![]() ).
).
(3)如图③中,设A′B′交x轴于点K.
当A′在AB上时,∵OA=OA′,
∴∠OAA′=∠AA′O=30°,
∵∠OA′B′=30°,
∴∠AA′K=60°,
∴∠AKA′=90°,
∵OA′=![]() ,∠OA′K=30°,
,∠OA′K=30°,
∴OK=![]() OA′=
OA′=![]() ,A′K=
,A′K=![]() OK=
OK=![]() ,
,
∴A′(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势:
年份
2015
2016
2017
…
入学儿童人数
2520
2330
2140
…
(1)上表中_____是自变量,_____是因变量;
(2)你预计该地区从_____年起入学儿童的人数不超过2000人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市实行阶梯电价制度,居民家庭每月用电量不超过80千瓦时时,实行“基本电价”;当每月用电量超过80千瓦时时,超过部分实行“提高电价”.去年小张家4月用电量为100千瓦时,交电费68元;5月用电量为120千瓦时,交电费88元.则基本电价”是__元/千瓦时,“提高电价”是__元/千瓦时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距120km.甲、乙两辆汽车同时从A地出发去B地,已知甲车的速度是乙车速度的1.2倍,结果甲车比乙车提前20分钟到达,求甲车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
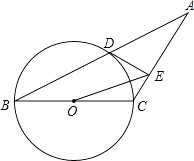
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形,当边长为n根火柴棍时,若摆出的正方形所用的火柴棍的根数为S,则S= (用含n的代数式表示,n为正整数).

-
科目: 来源: 题型:
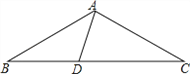
查看答案和解析>>【题目】(10分)如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.
相关试题

