【题目】如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接EF并延长,交CB的延长线于点G,连接BD.
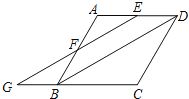
(1) 求证:四边形EGBD是平行四边形;
(2) 连接AG,若∠FGB=![]() ,GB=AE=3,求AG的长.
,GB=AE=3,求AG的长.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)依据菱形的性质及等式的性质,得![]() ,
,![]() ,由平行得
,由平行得![]() ∽
∽![]() ,依据相似的性质得到
,依据相似的性质得到![]() ,从而
,从而![]() ,依据一组对边平行且相等的四边形是平行四边形得到四边形EGBD是平行四边形;
,依据一组对边平行且相等的四边形是平行四边形得到四边形EGBD是平行四边形;
(2)先结合条件求得![]() =3,
=3,![]() ,由等边对等角得到
,由等边对等角得到![]() ,依据三角形外角的性质得到
,依据三角形外角的性质得到![]() ,作
,作![]() 于
于![]() ,运用锐角三角函数求出
,运用锐角三角函数求出![]() ,再求出
,再求出![]() ,最后用勾股定理求出AG的长.
,最后用勾股定理求出AG的长.
解:(1) 证明:∵菱形ABCD,
∴![]() ,
,![]() ,
,
又∵AE=AF,
∴![]() ,即
,即![]() ,
,![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形EGBD是平行四边形;
(2) ∵![]() ,GB=AE=3,AE=AF,
,GB=AE=3,AE=AF,
∴![]() =3,
=3,
∴![]() ,
,![]()
∴![]() ,
,
作![]() 于
于![]() ,
,
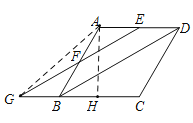
则![]() =
=![]() ,
,![]() =3,则
=3,则![]() ,
,
![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 坐标为
坐标为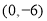 ,点
,点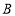 在
在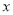 轴的负半轴上,点
轴的负半轴上,点 、
、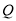 均在线段
均在线段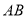 上,且
上,且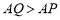 ,点
,点 的横坐标为
的横坐标为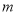 .在
.在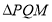 中,若
中,若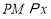 轴,
轴,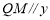 轴,则称
轴,则称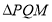 为点
为点 、
、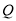 的“榕树三角形”.
的“榕树三角形”.(1)若点
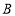 坐标为
坐标为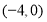 ,且
,且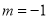 ,则点
,则点 、
、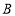 的“榕树三角形”的面积为 .
的“榕树三角形”的面积为 .(2)当点
 、
、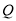 的“榕树三角形”是等腰三角形时,求点
的“榕树三角形”是等腰三角形时,求点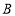 的坐标.
的坐标.(3)在(2)的条件下,作过
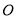 、
、 、
、 三点的抛物线
三点的抛物线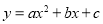 .
.①若
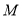 点必为抛物线上一点,求点
点必为抛物线上一点,求点 、
、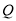 的“榕树三角形”面积
的“榕树三角形”面积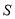 与
与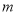 之间的函数关系式.
之间的函数关系式.②当点
 、
、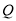 的“榕树三角形”面积2,且抛物线
的“榕树三角形”面积2,且抛物线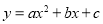 与点
与点 、
、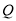 的“榕树三角形”恰有两个交点时,直接写出
的“榕树三角形”恰有两个交点时,直接写出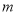 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】容器中有A,B,C 3种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗B粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子.例如,一颗A粒子和一颗B粒子发生碰撞则变成一颗C粒子.现有A粒子10颗,B粒子8颗,C粒子9颗,如果经过各种两两碰撞后,只剩1颗粒子.给出下列结论:
①最后一颗粒子可能是A粒子
②最后一颗粒子一定是C粒子
③最后一颗粒子一定不是B粒子
④以上都不正确
其中正确结论的序号是( ).(写出所有正确结论的序号)
A.①B.②③C.③D.①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦EF⊥AB于点C,过点F作⊙O的切线交AB的延长线于点D.
(1)已知∠A=α,求∠D的大小(用含α的式子表示);
(2)取BE的中点M,连接MF,请补全图形;若∠A=30°,MF=
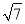 ,求⊙O的半径.
,求⊙O的半径.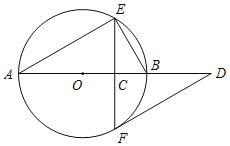
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,函数
 (x>0)的图象与直线l1:
(x>0)的图象与直线l1: 交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.
交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.
(1) 当点A的横坐标为1时,则此时k的值为 _______;
(2) 横、纵坐标都是整数的点叫做整点. 记函数
 (x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
(x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.①当k=3时,结合函数图像,则区域W内的整点个数是_________;
②若区域W内恰有1个整点,结合函数图象,直接写出k的取值范围:___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2.
(1)请用含有b的代数式表示c: ;
(2)若点B在直线l上,且B的横坐标为-1,点C的坐标为(b,5).
①若抛物线M还过点B,直接写出该抛物线的解析式;
②若抛物线M与线段BC恰有一个交点,结合函数图象,直接写出b的取值范围.
相关试题

