【题目】如图所示,正比例函数y= ![]() x的图象与反比例函数y=
x的图象与反比例函数y= ![]() (k≠0)在第一象限的图象交于点
(k≠0)在第一象限的图象交于点 ![]() ,过点A作X轴的垂线,垂足为M,已知△AOM的面积为1.
,过点A作X轴的垂线,垂足为M,已知△AOM的面积为1.
(1)求反比例函数的解析式;
(2)如果点 ![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点 ![]() 与点
与点 ![]() 不重合),且点
不重合),且点 ![]() 的横坐标为1,在
的横坐标为1,在 ![]() 轴上求一点
轴上求一点 ![]() ,使
,使 ![]() 最小.
最小.
参考答案:
【答案】
(1)解:根据题意可设A点的坐标为(a,b),则b= ![]() .∴ab=k .
.∴ab=k .
∵△AOM的面积为1.
∴ ![]() ab=1 ,
ab=1 ,
∴ ![]() k=1 .
k=1 .
∴ k=2.
∴ 反比例函数的解析式为y= ![]()
(2)解:由 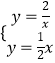 得
得 ![]() 或
或 ![]() ,
,
∵A在第一象限,
∴ A为(2,1),设A点关于x轴的对称点为C,
则C点的坐标为(2,-1)如要在x轴上求一点P,使PA+PB最小.
则P点应为BC和x轴的交点,
如图所示.设直线BC的解析式为y=mx+n.
∵ B为(1,2),
∴ ![]() ,解得:
,解得: ![]() ,
,
∴ BC的解析式为y=-3x+5.
当y=0时,-3x+5=0,x=-![]() ,
,
∴ P点坐标为( -![]() ,0)
,0)
【解析】(1)根据题意可设A点的坐标为(a,b),△AOM的面积为1,由反比例函数的k的几何意义,可得出ab=2,即|k|=2,k>0,即可求出反比例函数的解析式。
(2)要在x轴上求作一点P,而A、B两点的x轴的同一侧,作点A关于x轴的对称点C,连接BC交x轴于点P,先求出点C和点B的坐标,再求出直线BC的函数解析式,然后求出当y=0时,x的值,即可求出点P饿坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对轴对称-最短路线问题的理解,了解已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋子中装有大小完全相同的3粒乒乓球,其中2粒白色,1粒黄色.请你用它为甲、乙两位同学设计一个能决定胜负的公平的摸球游戏规则.并说明公平的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD和四边形ECGF都是正方形,点C、D、E在一条直线上,点B、C、G在一条直线上.
(1)写出表示阴影部分面积的表达式(结果要求化简);
(2)当
 求阴影面积的面积
求阴影面积的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】(给出定义)
数轴上顺次有三点A、C、B,若点C到点A的距离是点C到点B的距离的3倍,我们就称点C是(A、B)的“梦想点”例如:图①中,点A、B表示的数分别为-2、2,表示数1的点C是(A、B)的“梦想点”;图②中,点A、B表示对的数分别为-2、2,表示-1的点C是(B、A)的“梦想点.

(解决问题)
(1)若数轴上M、N两点所表示的数分别为
 且
且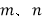 满足
满足 求出(M、N)的“梦想点”表示的数;
求出(M、N)的“梦想点”表示的数;(2)如图③,在数轴上点A、B表示的数分别为-15和65,点P从点A出发沿数轴向右运动:
①若点P运动到点B停止,则当P、A、B中恰好有一个点为其余两个点的“梦想点”时,求这个点表示的数;
②若点P运动到B后,继续沿数轴向右运动的过程中,是否还存在点P、A、B中恰好有一个点为其余两点的“梦想点”的情况?若存在,请直接写出此时以PA、PB为邻边长的长方形的周长;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣
 ﹣(+13)+(﹣
﹣(+13)+(﹣ )﹣(﹣17)
)﹣(﹣17)(2)﹣22+3÷(﹣1)2017﹣|﹣4|×5
(3)先化简再求值﹣3(2x2﹣xy)+4(x2+xy﹣6),其中x=﹣1,y=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给的信息解答下列问题:

(1)这次评价中,一共抽查了名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有小正方形的边长都为1,A、B、C都在格点上.
(1)过点C画直线AB的平行线(不写作法,下同);
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.
(3)线段 的长度是点A到直线BC的距离,线段AH的长度是点 到直线 的距离.
(4)因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段AG、AH的大小关系为AG AH.

相关试题

