【题目】一个袋子中装有大小完全相同的3粒乒乓球,其中2粒白色,1粒黄色.请你用它为甲、乙两位同学设计一个能决定胜负的公平的摸球游戏规则.并说明公平的理由.
参考答案:
【答案】解:先看两次摸取实验共有多少种等可能结果,可从袋子中摸出一粒球,记录其颜色,放回,搅匀,再从袋子中摸出一球;列树形图如下:  从树形图可知,共有9种可能,且都是等可能,其中两粒都是白色的有4种可能,即(白1,白1),(白1,白2),(白2,白1)(白2,白2),一粒黄色一粒白色的有4种可能,即(白1,黄),(白2,黄),(黄,白1)(黄,白2),所以游戏规则可设置为:若摸取的两粒都是白色,则甲胜;若摸取的两粒为一粒黄色一粒白色,则乙胜.因为
从树形图可知,共有9种可能,且都是等可能,其中两粒都是白色的有4种可能,即(白1,白1),(白1,白2),(白2,白1)(白2,白2),一粒黄色一粒白色的有4种可能,即(白1,黄),(白2,黄),(黄,白1)(黄,白2),所以游戏规则可设置为:若摸取的两粒都是白色,则甲胜;若摸取的两粒为一粒黄色一粒白色,则乙胜.因为 ![]() ,
, ![]() .∴此游戏公平.
.∴此游戏公平.
【解析】先根据从袋子中摸出一粒球,记录其颜色,放回,搅匀,再从袋子中摸出一球,列出树状图,再求出所有等可能的结果数,再观察发现其中两粒都是白色的有4种可能,一粒黄色一粒白色的有4种可能,即可设置游戏为若摸取的两粒都是白色,则甲胜;若摸取的两粒为一粒黄色一粒白色,则乙胜。
【考点精析】解答此题的关键在于理解列表法与树状图法的相关知识,掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDF;
(2)若AB=4,BC=8,求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
 的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3)
的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3)
①画出△ABC关于 x轴对称的△A1B1C1;
x轴对称的△A1B1C1;
②以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD和四边形ECGF都是正方形,点C、D、E在一条直线上,点B、C、G在一条直线上.
(1)写出表示阴影部分面积的表达式(结果要求化简);
(2)当
 求阴影面积的面积
求阴影面积的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】(给出定义)
数轴上顺次有三点A、C、B,若点C到点A的距离是点C到点B的距离的3倍,我们就称点C是(A、B)的“梦想点”例如:图①中,点A、B表示的数分别为-2、2,表示数1的点C是(A、B)的“梦想点”;图②中,点A、B表示对的数分别为-2、2,表示-1的点C是(B、A)的“梦想点.

(解决问题)
(1)若数轴上M、N两点所表示的数分别为
 且
且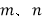 满足
满足 求出(M、N)的“梦想点”表示的数;
求出(M、N)的“梦想点”表示的数;(2)如图③,在数轴上点A、B表示的数分别为-15和65,点P从点A出发沿数轴向右运动:
①若点P运动到点B停止,则当P、A、B中恰好有一个点为其余两个点的“梦想点”时,求这个点表示的数;
②若点P运动到B后,继续沿数轴向右运动的过程中,是否还存在点P、A、B中恰好有一个点为其余两点的“梦想点”的情况?若存在,请直接写出此时以PA、PB为邻边长的长方形的周长;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正比例函数y=
 x的图象与反比例函数y=
x的图象与反比例函数y=  (k≠0)在第一象限的图象交于点
(k≠0)在第一象限的图象交于点  ,过点A作X轴的垂线,垂足为M,已知△AOM的面积为1.
,过点A作X轴的垂线,垂足为M,已知△AOM的面积为1.
(1)求反比例函数的解析式;
(2)如果点 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点  与点
与点  不重合),且点
不重合),且点  的横坐标为1,在
的横坐标为1,在  轴上求一点
轴上求一点  ,使
,使  最小.
最小.
相关试题

