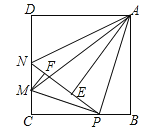
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有 (写出所有正确结论的序号)
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为![]() ;
;
⑤当△ABP≌△ADN时,BP=![]() .
.
参考答案:
【答案】①②⑤.
【解析】
试题分析:①正确,只要证明∠APM=90°即可解决问题.
②正确,设PB=x,构建二次函数,利用二次函数性质解决问题即可.
③错误,设ND=NE=y,在RT△PCN中,利用勾股定理求出y即可解决问题.
④错误,作MG⊥AB于G,因为AM=![]() =
=![]() ,所以AG最小时AM最小,构建二次函数,求得AG的最小值为3,AM的最小值为5.
,所以AG最小时AM最小,构建二次函数,求得AG的最小值为3,AM的最小值为5.
⑤正确,在AB上取一点K使得AK=PK,设PB=z,列出方程即可解决问题.
试题解析:∵∠APB=∠APE,∠MPC=∠MPN,∵∠CPN+∠NPB=180°,∴2∠NPM+2∠APE=180°,∴∠MPN+∠APE=90°,∴∠APM=90°,∵∠CPM+∠APB=90°,∠APB+∠PAB=90°,∴∠CPM=∠PAB,∵四边形ABCD是正方形,∴AB=CB=DC=AD=4,∠C=∠B=90°,∴△CMP∽△BPA.故①正确,设PB=x,则CP=4﹣x,∵△CMP∽△BPA,∴![]() ,∴CM=
,∴CM=![]() x(4﹣x),∴S四边形AMCB=
x(4﹣x),∴S四边形AMCB=![]() [4+
[4+![]() x(4﹣x)]×4=
x(4﹣x)]×4=![]() =
=![]() ,∴x=2时,四边形AMCB面积最大值为10,故②正确,当PB=PC=PE=2时,设ND=NE=y,在RT△PCN中,
,∴x=2时,四边形AMCB面积最大值为10,故②正确,当PB=PC=PE=2时,设ND=NE=y,在RT△PCN中,![]() 解得
解得![]() ,∴NE≠EP,故③错误,作MG⊥AB于G,∵AM=
,∴NE≠EP,故③错误,作MG⊥AB于G,∵AM=![]() =
=![]() ,∴AG最小时AM最小,∵AG=AB﹣BG=AB﹣CM=4﹣
,∴AG最小时AM最小,∵AG=AB﹣BG=AB﹣CM=4﹣![]() x(4﹣x)=
x(4﹣x)=![]() ,∴x=1时,AG最小值=3,∴AM的最小值=
,∴x=1时,AG最小值=3,∴AM的最小值=![]() =5,故④错误.
=5,故④错误.
∵△ABP≌△ADN时,∴∠PAB=∠DAN=22.5°,在AB上取一点K使得AK=PK,设PB=z,∴∠KPA=∠KAP=22.5°.∵∠PKB=∠KPA+∠KAP=45°,∴∠BPK=∠BKP=45°,∴PB=BK=z,AK=PK=![]() z,∴z+
z,∴z+![]() z=4,∴z=
z=4,∴z=![]() ,∴PB=
,∴PB=![]() 故⑤正确.
故⑤正确.
故答案为:①②⑤.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为 cm2.
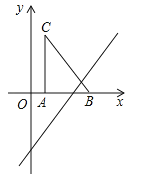
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品降价20%后出售,一段时间后欲恢复原价,则应在售价的基础上提高的百分数为_____%.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(5+i)×(3﹣4i)=19﹣17i.
(1)填空:i3= ,i4= .
(2)计算:(4+i)2.
(3)试一试:请利用以前学习的有关知识将
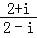 化简成a+bi的形式.
化简成a+bi的形式. -
科目: 来源: 题型:
查看答案和解析>>【题目】填空题
(1)若ab,则b<a,即不等式具有对称性;
(2)若a>b,b>c,则ac,即不等式具有同向传递性. -
科目: 来源: 题型:
查看答案和解析>>【题目】当x=4时,式子5(x+b)﹣10与bx+4x的值相等,则b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子:①-3<0;②4x+5>0;③x=3;④x2+x;⑤x≠-4;⑥x+2>x+1.其中是不等式的有( )
A.2个
B.3个
C.4个
D.5个
相关试题

