【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,c满足![]() +(c-8)2=0.
+(c-8)2=0.
![]()
(1) a = ,b = ,c = .
(2) 若将数轴折叠,使得A点与B点重合,则点C与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和8个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB = ,AC = ,BC = .(用含t的代数式表示)
(4) 请问:3AB-(2BC+AC)的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
参考答案:
【答案】见解析
【解析】试题分析:(1)、首先根据非负数的性质以及有理数的性质得出a、b、c的值;(2)、根据折叠的性质得出答案;(3)、在数轴上向右运动,则加上几个单位长度,向左运动则减去几个单位长度,根据运动的速度分别得出AB、AC和BC的长度;(4)、根据题意得出代数式为一个定值,即不会随着时间的改变为改变.
试题解析:(1)a= -2 ,b= 1 ,c= 8 ;
(2) -9
(3) AB= 6t+3 ,AC= 10t+10 ,BC= 4t+7 ;
(4)结论:3AB-(2BC+AC)的值不随着时间t的变化而改变
理由:3AB-(2BC+AC)=3(6t+3)-[2(4t+7)+(10t+10)]=-15
所以3AB-(2BC+AC)的值不随着时间t的变化而改变
-
科目: 来源: 题型:
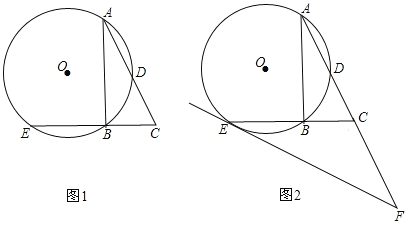
查看答案和解析>>【题目】(2016四川省乐山市第25题)已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O于点E.
(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;
(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.
①若CF=CD时,求sin∠CAB的值;
②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解(x+y)2﹣2(x2﹣y2)+(x﹣y)2的结果为( )
A.4(x﹣y)2B.4x2C.4(x+y)2D.4y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的一个外角是45°,则该正多边形从一个顶点出发的对角线的条数为( )
A.4B.5C.6D.8
-
科目: 来源: 题型:
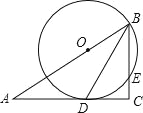
查看答案和解析>>【题目】(2016广西省南宁市第21题)在图“书香八桂,阅读圆梦”读数活动中,某中学设置了书法、国学、诵读、演讲、征文四个比赛项目如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题。

(1)在第4个图中,共有白色瓷砖 块;在第
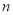 个图中,共有白色瓷砖 块;
个图中,共有白色瓷砖 块;(2)在第4个图中,共有瓷砖 块;在第
 个图中,共有瓷砖 块;
个图中,共有瓷砖 块;(3)如果每块黑瓷砖4元,白瓷砖3元,铺设当
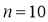 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖? -
科目: 来源: 题型:
查看答案和解析>>【题目】数据1460000000用科学记数法表示应是 .
相关试题

