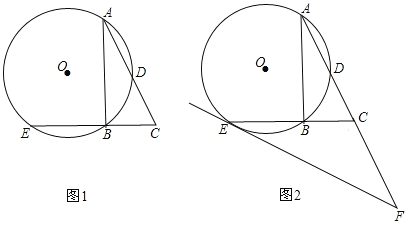
【题目】(2016四川省乐山市第25题)已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O于点E.
(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;
(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.
①若CF=CD时,求sin∠CAB的值;
②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)
参考答案:
【答案】(1)AE=CE;(2)①![]() ;②
;②![]() .
.
【解析】
试题分析:(1)连接AE、DE,如图1,根据圆周角定理可得∠ADE=∠ABE=90°,由于AD=DC,根据垂直平分线的性质可得AE=CE;
(2)连接AE、ED,如图2,由∠ABE=90°可得AE是⊙O的直径,根据切线的性质可得∠AEF=90°,从而可证到△ADE∽△AEF,然后运用相似三角形的性质可得![]() =ADAF.①当CF=CD时,可得
=ADAF.①当CF=CD时,可得![]() ,从而有EC=AE=
,从而有EC=AE=![]() CD,在Rt△DEC中运用三角函数可得sin∠CED=
CD,在Rt△DEC中运用三角函数可得sin∠CED=![]() ,根据圆周角定理可得∠CAB=∠DEC,即可求出sin∠CAB的值;②当CF=aCD(a>0)时,同①即可解决问题.
,根据圆周角定理可得∠CAB=∠DEC,即可求出sin∠CAB的值;②当CF=aCD(a>0)时,同①即可解决问题.
试题解析:(1)AE=CE.理由:
连接AE、DE,如图1,∵∠ABC=90°,∴∠ABE=90,∴∠ADE=∠ABE=90°,∵AD=DC,∴AE=CE;
(2)连接AE、ED,如图2,∵∠ABE=90°,∴AE是⊙O的直径,∵EF是⊙OO的切线,∴∠AEF=90°,∴∠ADE=∠AEF=90°,又∵∠DAE=∠EAF,∴△ADE∽△AEF,∴![]() ,∴
,∴![]() =ADAF.
=ADAF.
①当CF=CD时,AD=DC=CF,AF=3DC,∴![]() =DC3DC=
=DC3DC=![]() ,∴AE=
,∴AE=![]() DC,∵EC=AE,∴EC=
DC,∵EC=AE,∴EC=![]() DC,∴sin∠CAB=sin∠CED=
DC,∴sin∠CAB=sin∠CED=![]() =
=![]() =
=![]() ;
;
②当CF=aCD(a>0)时,sin∠CAB=![]() .
.
∵CF=aCD,AD=DC,∴AF=AD+DC+CF=(a+2)CD,∴![]() =DC(a+2)DC=(a+2)
=DC(a+2)DC=(a+2)![]() ,∴AE=
,∴AE=![]() DC,∵EC=AE,∴EC=
DC,∵EC=AE,∴EC=![]() DC,∴sin∠CAB=sin∠CED=
DC,∴sin∠CAB=sin∠CED=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上到–1的点的距离是3的点所表示的数为
A. 2 B. –4 C. –4或2 D. –2或4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为有理数,且它们在数轴上的位置如图所示.
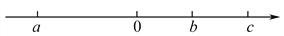
(1)试判断a,b,c的正负性;
(2)在数轴上标出a,b,c的相反数的位置;
(3)根据数轴化简:
①|a|=_______;②|b|=____;
③|c|=____;④|-a|=_______;
⑤|-b|=____;⑥|-c|=____.
(4)若|a|=5.5,|b|=2.5,|c|=5,求a,b,c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产一批精密的零件要求是φ50
 (φ表示圆形工件的直径,单位是mm),抽查了5个零件,数据如下表,超过规定的记作正数,不足的记作负数.
(φ表示圆形工件的直径,单位是mm),抽查了5个零件,数据如下表,超过规定的记作正数,不足的记作负数.
(1)哪些产品是符合要求的?
(2)符合要求的产品中哪个质量最好?用绝对值的知识加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解(x+y)2﹣2(x2﹣y2)+(x﹣y)2的结果为( )
A.4(x﹣y)2B.4x2C.4(x+y)2D.4y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的一个外角是45°,则该正多边形从一个顶点出发的对角线的条数为( )
A.4B.5C.6D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,c满足
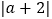 +(c-8)2=0.
+(c-8)2=0.
(1) a = ,b = ,c = .
(2) 若将数轴折叠,使得A点与B点重合,则点C与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和8个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB = ,AC = ,BC = .(用含t的代数式表示)
(4) 请问:3AB-(2BC+AC)的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
相关试题

