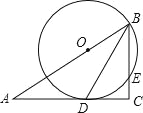
【题目】(2016广西省南宁市第21题)在图“书香八桂,阅读圆梦”读数活动中,某中学设置了书法、国学、诵读、演讲、征文四个比赛项目如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
参考答案:
【答案】(1)、证明过程见解析;(2)、12.
【解析】
试题分析:(1)、连接OD,由BD为角平分线得到一对角相等,根据OB=OD,等边对等角得到一对角相等,等量代换得到一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODA为直径,即可得证;(2)、由OD与BC平行得到三角形OAD与三角形BAC相似,由相似得比例求出OA的长,进而确定出AB的长,连接EF,过O作OG垂直于BC,利用勾股定理求出BG的长,由BG+GC求出BC的长,再由三角形BEF与三角形BAC相似,由相似得比例求出BE的长即可.
试题解析:(1)、连接OD, ∵BD为∠ABC平分线, ∴∠1=∠2, ∵OB=OD, ∴∠1=∠3, ∴∠2=∠3,
∴OD∥BC, ∵∠C=90°, ∴∠ODA=90°, 则AC为圆O的切线;
(2)、过O作OG⊥BC, ∴四边形ODCG为矩形, ∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6, ∴BC=BG+GC=6+10=16, ∵OD∥BC,
∴△AOD∽△ABC, ∴![]() =
=![]() ,即
,即![]() =
=![]() , 解得:OA=
, 解得:OA=![]() , ∴AB=
, ∴AB=![]() +10=
+10=![]() ,
,
连接EF, ∵BF为圆的直径, ∴∠BEF=90°, ∴∠BEF=∠C=90°, ∴EF∥AC,
∴![]() =
=![]() ,即
,即![]() =
=![]() , 解得:BE=12.
, 解得:BE=12.

-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解(x+y)2﹣2(x2﹣y2)+(x﹣y)2的结果为( )
A.4(x﹣y)2B.4x2C.4(x+y)2D.4y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的一个外角是45°,则该正多边形从一个顶点出发的对角线的条数为( )
A.4B.5C.6D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,c满足
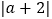 +(c-8)2=0.
+(c-8)2=0.
(1) a = ,b = ,c = .
(2) 若将数轴折叠,使得A点与B点重合,则点C与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和8个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB = ,AC = ,BC = .(用含t的代数式表示)
(4) 请问:3AB-(2BC+AC)的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题。

(1)在第4个图中,共有白色瓷砖 块;在第
 个图中,共有白色瓷砖 块;
个图中,共有白色瓷砖 块;(2)在第4个图中,共有瓷砖 块;在第
 个图中,共有瓷砖 块;
个图中,共有瓷砖 块;(3)如果每块黑瓷砖4元,白瓷砖3元,铺设当
 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖? -
科目: 来源: 题型:
查看答案和解析>>【题目】数据1460000000用科学记数法表示应是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两堆规格完全相同的课本整齐叠放在讲台上.请根据图中所给出的数据信息,回答下面的问题:
(1)每本课本的厚度为________cm;
(2)若有一摞上述规格的课本
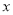 本,整齐叠放在讲台上,请用含
本,整齐叠放在讲台上,请用含 的代数式表示出这一摞课本的顶部距离地面的高度.
的代数式表示出这一摞课本的顶部距离地面的高度.(3)当
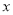 =30时,若从中取走12本,求余下的课本的顶部距离地面的高度.
=30时,若从中取走12本,求余下的课本的顶部距离地面的高度.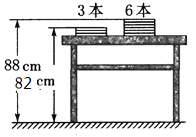
相关试题

