【题目】折叠矩形纸片:
第一步,如图1,在纸片一端折出一个正方形MBCN,再把纸片展开;
第二步,如图2,把这个正方形对折,再把纸片展开,得矩形MAEN和ABCE;
第三步,如图3,折出矩形ABCE的对角线EB,并把EB折到图中所示的ED处;
第四步,如图4,展平纸片,按所得点D折出DF,得矩形BFDC.
(1)若MN=2时,CM=________;
(2)![]() 的值为 ________.
的值为 ________.

参考答案:
【答案】![]()
![]()
【解析】
(1)由等腰直角三角形的性质和勾股定理,即可求出CM的长度;
(2)设正方形的边长为2a,由折叠的性质,可得EC=正方形的边长×![]() ,在Rt△ABC中,利用勾股定理可求出AB与正方形的边长之间的关系,再求出CD=
,在Rt△ABC中,利用勾股定理可求出AB与正方形的边长之间的关系,再求出CD=![]() ,即可求解.
,即可求解.
解:(1)∵四边形MBCN是正方形,MC是对角线,
∴MN=CN=2,
由勾股定理,得:![]() ;
;
故答案为:![]() ;
;
(2)在正方形BCNM中,设NC=2a=BC,
∵E为NC的中点,
∴EC=![]() .
.
在Rt△EBC中,EB=![]() .
.
又∵ED=EB,
∴CD=ED![]() EC=(
EC=(![]() )a.
)a.
∴![]() ;
;
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=(AD2+AB2),其中结论正确的个数是( )
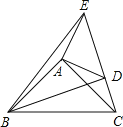
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中, AB=10,AD=5 ,CD=12.连接AC,若AC=BC=13,则四边形ABCD的面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=__________.
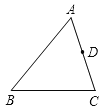
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑自行车去郊外春游,他离家的距离y(千米)与所用时间x(小时)之间的关系如图,根据图象回答:
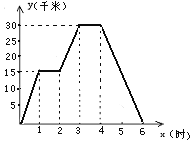
(1)小明到达离家最远的地方需几小时?此时离家多远?
(2)小明出发两个半小时时离家多远?
(3)小明出发多长时间离家12.5千米?
相关试题

