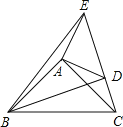
【题目】已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=(AD2+AB2),其中结论正确的个数是( )
A.1B.2C.3D.4
参考答案:
【答案】C
【解析】
①由AB=AC,AD=AE,利用等式的性质得到夹角相等,利用SAS得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到BD=CE;
②由三角形ABD与三角形ACE全等,得到一对角相等,再利用等腰直角三角形的性质及等量代换得到BD垂直于CE;
③由等腰直角三角形的性质得到∠ABD+∠DBC=45°,等量代换得到∠ACE+∠DBC=45°;
④由BD垂直于CE,在直角三角形BDE中,利用勾股定理列出关系式,等量代换即可作出判断.
解:如图:

①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
∵在△BAD和△CAE中,
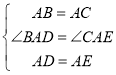 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,故①正确;
②∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE,故②正确;
③∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠ABD+∠DBC=45°,
∵∠ABD=∠ACE,
∴∠ACE+∠DBC=45°,故③正确;
④∵BD⊥CE,
∴在Rt△BDE中,利用勾股定理得:
BE2=BD2+DE2,
∵△ADE为等腰直角三角形,
∴DE=![]() AD,
AD,
即DE2=2AD2,
∴BE2=BD2+DE2=BD2+2AD2,
∴BE2≠AD2+AB2,故④错误,
综上,正确的个数为3个.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y= kx+b的图象与反比例函数
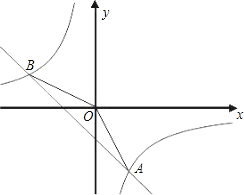
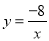 的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:(1)求这个一次函数的解析式;
(2)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分6分)
(1)(3分)(-3)2-|-
 |+(3.14-x)0
|+(3.14-x)0(2)(4分)先化简,再求值:[(2x-y)2+(2x-y)(2x+y)]÷(4x),其中x=2,y=-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中, AB=10,AD=5 ,CD=12.连接AC,若AC=BC=13,则四边形ABCD的面积为_____.

-
科目: 来源: 题型:
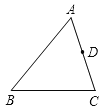
查看答案和解析>>【题目】如图,在三角形ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】折叠矩形纸片:
第一步,如图1,在纸片一端折出一个正方形MBCN,再把纸片展开;
第二步,如图2,把这个正方形对折,再把纸片展开,得矩形MAEN和ABCE;
第三步,如图3,折出矩形ABCE的对角线EB,并把EB折到图中所示的ED处;
第四步,如图4,展平纸片,按所得点D折出DF,得矩形BFDC.
(1)若MN=2时,CM=________;
(2)
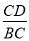 的值为 ________.
的值为 ________. 
相关试题

