搜索
【题目】如图，在长方形 ABCD 中，放入六个形状大小相同的长方形，所标尺寸如图所示， 则图中阴影部分面积为（ ）
A. 44cm2B. 36cm2C. 96 cm2D. 84cm2
参考答案：
【答案】A
【解析】
本题通过图像发现小长方形和大长方形的长和宽的联系从而列式，设长方形的长和宽为未知数，根据图示可得到关于x，y的两个方程，可求得解，从而可得到大长方形的面积，再根据阴影部分的面积=大长方形的面积-6个小长方形的面积求解即可.
设小长方形的长为x，宽为y，如图可知，
x+3y=14，①
x+y-2y=6，即x-y=6，②
①-②得4y=8，y=2，
代入②得x=8，
因此，大矩形ABCD的宽AD=6+2y=6+2×2=10．
矩形ABCD面积=14×10=140（平方厘米），
阴影部分总面积=140-6×2×8=44（平方厘米）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直角三角形的斜边
在
轴的正半轴上，点
与原点重合，点
的坐标是
，且
，若将
绕着点
旋转后30°，点和
点分别落在点
和点
处，那么直线
的解析式是__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】节能灯在城市已基本普及，今年某省面向县级及农村地区推广，为相应号召，某商场计划用3800元购进节能灯120只，这两种节能灯的进价、售价如下表：
（1）求甲、乙两种节能灯各进多少只？
（2）全部售完120只节能灯后，该商场获利润多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
上有
、
两点，
，点
是线段
上的一点，OA=2OB.（1）
________
，
________；（2）若点C是线段AB上一点，且满足
，求CO的长；（3）若动点
、
分别从点、同时出发，在直线上向右运动.点P的速度为
，点的速度为
，设动点、运动的时间为
，当点与点重合时，、两点都停止运动，求当
为何值时，
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，E为BC边上一点，且AB＝AE．
（1）求证：AC＝ED；
（2）若AE平分∠DAB，∠EAC＝25°，求∠AED的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形 ABCD 中，∠A=160°，∠B=50°，∠ADC、∠BCD 的平分线相交于点E，则∠CED=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】[数学实验探索活动]
实验材料现有若干块如图①所示的正方形和长方形硬纸片．
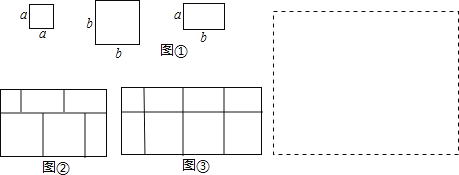
实验目的：
用若干块这样的正方形和长方形硬纸片拼成一个新的长方形，通过不同的方法计算面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径．
例如，选取正方形、长方形硬纸片共 6 块，拼出一个如图②的长方形，计算它的面积， 写出相应的等式有 a2+3ab+2b2=(a+2b)(a+b)或 (a+2b)(a+b) =a2+3ab+2b2．
问题探索：
(1) 小明想用拼图的方法解释多项式乘法(2a+b)(a+b) =2a2+3ab+b2 ，那么需要两种正方形纸片 张，长方形纸片 张；
(2)选取正方形、长方形硬纸片共 8 块，可以拼出一个如图③的长方形，计算图③的面积，并写出相应的等式；
(3)试借助拼图的方法，把二次三项式 2a2+5ab+2b2 分解因式，并把所拼的图形画在虚线方框内.
相关试题
