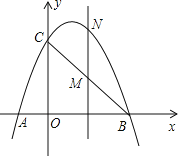
【题目】如图，已知抛物线经过点A(－1,0)、B(3,0)、C(0,3)三点。

(1)求抛物线的解析式。

(2)点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N若点M的横坐标为m，请用m的代数式表示MN的长。

(3)在（2）的条件下，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由。

参考答案：

【答案】(1)y=﹣x2+2x+3．(2) ﹣m2+3m（0＜m＜3）．(3) 当m=时，△BNC的面积最大，最大值为．

【解析】试题分析：（1）利用待定系数法求二次函数的解析式；
（2）先求直线BC的解析式，表示出M、N两点的坐标，利用纵坐标的差计算MN的长即可；
（3）根据面积公式得：S△BNC=S△CMN+S△MNB=|MN||OB|，OB的长是定值为3，所以MN的最大值即为面积的最大值，求MN所表示的二次函数的最值即可．

解：(1) ∵抛物线经过点A(1,0),B(3,0),C(0,3)三点，

∴设抛物线的解析式为：y=a(x+1)(x3)，

把C(0,3)代入得：3=a(0+1)(03)，

a=1，

∴抛物线的解析式：y＝－x2＋2x＋3

(2) 设直线BC的解析式为：y=kx+b，

把B(3,0),C(0,3)代入得： ，

解得：

，

∴直线BC的解析式为y＝－x＋3，

∴M(m，－m＋3)，

又∵MN⊥x轴，

∴N(m，－m2＋2m＋3)，

∴MN＝(－m2＋2m＋3)－(－m＋3)＝－m2＋3m(0＜m＜3)

(3)S△BNC＝S△CMN＋S△MNB＝|MN|·|OB|，

∴当|MN|最大时，△BNC的面积最大，

MN＝－m2＋3m＝－(m－)2＋，

所以当m＝时，△BNC的面积最大为××3＝

关闭