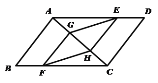
【题目】已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在AC上,且AE=CF,AH=CG.
求证:四边形EGFH是平行四边形.
参考答案:
【答案】见解析
【解析】
先根据平行四边形的性质得到AD∥BC,进而有∠EAH=∠FCG,再证明△AHE≌△CGF,利用全等三角形的性质和直线平行的判定得到FG∥EH,再根据平行四边形的判定定理即可证明;
证明:∵ABCD为平行四边形,
∴AD∥BC(平行四边形对边平行)
∴∠EAH=∠FCG(两直线平行,内错角相等).
又∵AE=CF,AH=CG,
∴△AHE≌△CGF(SAS).
∴EH=FG,∠FGH=∠EHG(全等三角形对应边相等,对应角相等).
∴FG∥EH(内错角相等,两直线平行).
∴四边形GEHF为平行四边形(一组对边平行且相等的四边形是平行四边形).
-
科目: 来源: 题型:
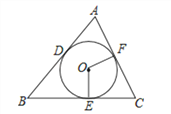
查看答案和解析>>【题目】如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,S△ABC=10cm2,C△ABC=10cm且∠C=60°.求:
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线相交于点O,AC=AB, E是AB边的中点,G、F为 BC上的点,连接OG和EF,若AB=13, BC=10,GF=5,则图中阴影部分的面积为( )
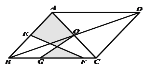
A.48B.36C.30D.24
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.

(1)请写出两个不同的正确结论;
(2)若CB=8,ED=2,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵8元,用300元购买甲种商品的件数恰好与用250元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共80件,且投入的经费不超过3600元,那么,最多可购买多少件甲种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=
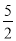 S△ABF.其中正确的结论有( )
S△ABF.其中正确的结论有( ) 
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了如图两幅不完整的统计图:
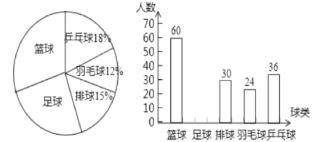
请根据以上统计图提供的信息,解答下列问题:
(1)共抽取___名学生进行问卷调查;
(2)补全条形统计图,求出扇形统计图中“篮球”所对应的圆心角的度数;
(3)该校共有2500名学生,请估计全校学生喜欢足球运动的人数。
相关试题

