【题目】如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.

(1)请写出两个不同的正确结论;
(2)若CB=8,ED=2,求⊙O的半径.
参考答案:
【答案】(1)答案不唯一,见解析(2)5
【解析】
试题分析:(1)可以从线段的关系、角的关系、三角形的关系等等方面说明;(2)设的半径等于R,利用垂经定理和勾股定理可求出圆的半径.
试题解析:(1)不同类型的正确结论有:①BE=CE;②BD=CD;③∠BED=90°;④∠BOD=∠A;⑤AC//OD;⑥AC⊥BC;⑦![]() ;⑧
;⑧![]() ;⑨△BOD是等腰三角形;⑩
;⑨△BOD是等腰三角形;⑩![]() ;等等。
;等等。
(2)∵ OD⊥CB ∴BE=CE=![]() =4
=4
设的半径等于R,则OE=OD-DE=R-2
在Rt△OEB中,由勾股定理得,
![]() 即
即![]()
解得R=5
∴⊙O的半径为5
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每个内角均为140°,则这个多边形是( )
A.七边形B.八边形C.九边形D.十边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】台湾是我国最大的岛屿,总面积为35989.76平方千米,这个数据用科学记数法表示为_____平方千米(保留两位有效数字).
-
科目: 来源: 题型:
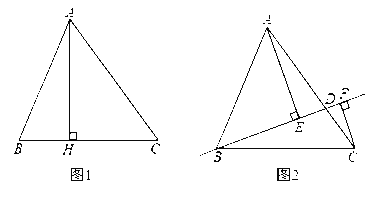
查看答案和解析>>【题目】如图1和2,在△ABC中,AB=13,BC=14,BH=5.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积
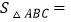 ;
;拓展:如图2,点D在AC上(可与点A,C重合),分别过点A.C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为
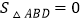 )
)(1)用含x,m,n的代数式表示
 及
及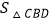 ;
;(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,直接写出这样的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.

(2)结论应用:① 如图2,点M,N在反比例函数
 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF. ② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段为边,能组成三角形的是().
A. 2cm,3cm,5cmB. 5cm,6cm,10cm
C. 1cm,1cm,3cmD. 3cm,4cm,9cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】若︱x-3︱+︱y+2︱=0,求yx的值。
相关试题

