【题目】为支持抗震救灾,我市A、B两地分别有赈灾物资100吨和180吨,需全部运往重灾区C、D两县,根据灾区的情况,这批赈灾物资运往C县的数量比运往D县的数量的2倍少80吨.
(1)求这批赈灾物资运往C、D两县的数量各是多少吨?
(2)设A地运往C县的赈灾物资数量为x吨(x为整数).若要B地运往C县的赈灾物资数量大于A地运往D县赈灾物资数量的2倍,且要求B地运往D县的赈灾物资数量不超过63吨,则A、B两地的赈灾物资运往C、D两县的方案有几种?
参考答案:
【答案】
(1)
解:)设运往C县的物资是a吨,D县的物资是b吨,
根据题意得, ![]() ,
,
解得 ![]() ,
,
答:这批赈灾物资运往C、D两县的数量各是160吨,120吨;
(2)
解:设A地运往C县的赈灾物资数量为x吨,则B地运往C县的物资是(160﹣x)吨,
A地运往D县的物资是(100﹣x)吨,B地运往D县的物资是120﹣(100﹣x)=(20+x)吨,
根据题意得, ![]() ,
,
解不等式①得,x>40,
解不等式②得,x≤43,
所以,不等式组的解集是40<x≤43,
∵x是整数,
∴x取41、42、43,
∴方案共有3种,分别为:
方案一:A地运往C县的赈灾物资数量为41吨,则B地运往C县的物资是119吨,
A地运往D县的物资是59吨,B地运往D县的物资是61吨;
方案二:A地运往C县的赈灾物资数量为42吨,则B地运往C县的物资是118吨,
A地运往D县的物资是58吨,B地运往D县的物资是62吨;
方案三:A地运往C县的赈灾物资数量为43吨,则B地运往C县的物资是117吨,
A地运往D县的物资是57吨,B地运往D县的物资是63吨
【解析】(1)设运往C县的物资是a吨,D县的物资是b吨,然后根据运往两地的物资总量列出一个方程,再根据运往C、D两县的数量关系列出一个方程,然后联立组成方程组求解即可;(2)根据A地运往C县的赈灾物资数量为x吨,表示出B地运往C县的物资是(160﹣x)吨,A地运往D县的物资是(100﹣x)吨,B地运往D县的物资是120﹣(100﹣x)=(20+x)吨,然后根据“B地运往C县的赈灾物资数量大于A地运往D县赈灾物资数量的2倍”列出一个不等式,根据“B地运往D县的赈灾物资数量不超过63吨”列出一个不等式,组成不等式组并求解,再根据x为整数即可得解.
【考点精析】解答此题的关键在于理解一元一次不等式组的应用的相关知识,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.
-
科目: 来源: 题型:
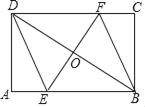
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)体育课上,某中学对七年级男生进行了引体向上测试,以能做7个为标准多于标准的次
数记为正数,不足的次数记为负数,其中8名男生的成绩为+2,-1,+3,0,-2,-3,+1,0.
(1)这8名男生中达到标准的占百分之几?
(2)他们共做了多少次引体向上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知P为⊙O外一点,PA为⊙O的切线,B为⊙O上一点,且PA=PB,C为优弧
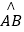 上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.
上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.
(1)求证:PB为⊙O的切线;
(2)若tan∠BCA= ,⊙O的半径为
,⊙O的半径为 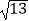 ,求弦AB的长.
,求弦AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑摩托车从邮局出发,先向西骑行2千米到达A村,继续向西骑行3千米到达B村,然后向东骑行9千米到达C村,最后回到邮局.
(1)C村离A村多远?
(2)若摩托车每10千米需1.5升汽油,邮递员最后回到邮局时,一共用了多少升汽油?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东24.5°方向,轮船向正东航行了2400m,到达Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.

(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(参考数据cos41°=0.75). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴与C、A两点,点B是x轴上一点,且横坐标为2,在OA上取一点H,使得OH=OB.
(1) 求点C的坐标.
(2) 求CH所在直线的表达式.
(3) 若点P在直线CH上运动,是否存在一点P,使得△PBC的面积是△AHB面积的
 ,若存在,求出点P的坐标,若不存在,说明理由.
,若存在,求出点P的坐标,若不存在,说明理由. 
相关试题

