【题目】设双曲线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在第三象限),将双曲线在第一象限的一支沿射线
在第三象限),将双曲线在第一象限的一支沿射线![]() 的方向平移,使其经过点
的方向平移,使其经过点![]() ,将双曲线在第三象限的一支沿射线
,将双曲线在第三象限的一支沿射线![]() 的方向平移,使其经过点
的方向平移,使其经过点![]() ,平移后的两条曲线相交于点
,平移后的两条曲线相交于点![]() ,
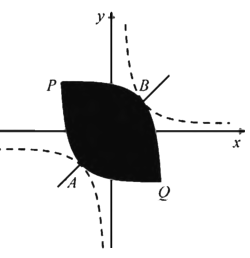
,![]() 两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,
两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,![]() 为双曲线的“眸径”.当双曲线
为双曲线的“眸径”.当双曲线![]() 的眸径为6时,
的眸径为6时,![]() 的值为__________.
的值为__________.
参考答案:
【答案】![]()
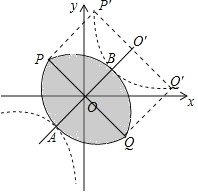
【解析】以PQ为边,作矩形PQQ′P′交双曲线于点P′、Q′,联立直线AB及双曲线解析式成方程组,通过解方程组可求出点A、B的坐标,由PQ的长度可得出点P的坐标(点P在直线y=-x上找出点P的坐标),由图形的对称性结合点A、B和P的坐标可得出点P′的坐标,再利用反比例函数图象上点的坐标特征即可得出关于k的一元一次方程,解之即可得出结论.
以PQ为边,作矩形PQQ′P′交双曲线于点P′、Q′,如图所示.
联立直线AB及双曲线解析式成方程组,![]() ,
,
解得: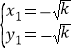 ,
,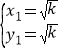 ,
,
∴点A的坐标为(-![]() ,-
,-![]() ),点B的坐标为(
),点B的坐标为(![]() ,
,![]() ).
).
∵PQ=6,
∴OP=3,点P的坐标为(-![]() ,
,![]() ).
).
根据图形的对称性可知:AB=OO′=PP′,
∴点P′的坐标为(-![]() +2
+2![]() ,
,![]() +2
+2![]() ).
).
又∵点P′在双曲线y=![]() 上,
上,
∴(-![]() +2
+2![]() )(
)(![]() +2
+2![]() )=k,
)=k,
解得:k=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级某班级为了促进同学养成良好的学习习惯,每天都对同学进行学规管理记分.如下是小李同学第8周学规得分(规定:加分为“+”,扣分为“﹣”).

(1)第8周小李学规得分总计是多少?
(2)根据班规,一学期里班级还会将同学每周的学规得分进行累加.已知小李同学第7周末学规累加分数为98分,若他在第9周末学规累加分数达到105分,则他第9周的学规得分总计是多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定,对数轴上的任意点P进行如下操作:先将点P表示的数乘以﹣1,再把所得数对应的点向右平移2个单位,得到点P的对应点P'.现对数轴上的点A,B进行以上操作,分别得到点A',B'.
(1)若点A对应的数是﹣2,则点A'对应的数x= ;若点B'对应的数是
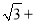 2,则点B对应的数y= .
2,则点B对应的数y= .(2)在(1)的条件下,求代数式
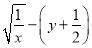 的值.
的值.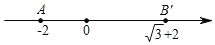
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
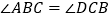 ,添加以下条件,不能判定
,添加以下条件,不能判定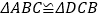 的是( )
的是( )
A.
 B.
B.  C.
C.  D.
D. 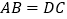
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+
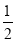 ∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-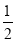 ∠A.上述说法正确的个数是( )
∠A.上述说法正确的个数是( ) 
A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 三边的中线 AD,BE,CF 相交于点 G,若 S△ABC=15,则图中阴影部分面积是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
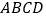 中,
中,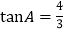 ,
,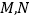 分别在边
分别在边 上,将四边形
上,将四边形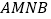 沿
沿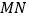 翻折,使
翻折,使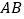 的对应线段
的对应线段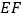 经过顶点
经过顶点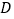 ,当
,当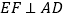 时,
时,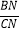 的值为__________.
的值为__________.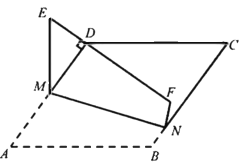
相关试题

