搜索
【题目】如图，在ABCD中，M、N是对角线BD上两点，且BN=DM．
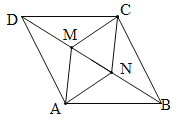
（1）求证：AM=CN；
（2）若AM⊥BD于M，AD=10，CN=6，求DM的长．
参考答案：
【答案】见解析；（2）DM=8.
【解析】
（1）根据平行四边形的性质及平行线的性质证明△ADM≌△CBN即可；
（2）根据全等三角形对应边相等得出AM的长．在Rt△AMD中，由勾股定理即可得出结论．
（1）∵ABCD是平行四边形，∴AD=BC，AD∥BC，∴∠ADB=∠CBD．
在△ADM与△CBN中，∵AD=BC，∠ADB=∠CBD，DM=BN，∴△ADM≌△CBN，∴AM=CN；
（2）∵△ADM≌△CBN，∴AM=CN．
∵CN=6，∴AM=CN=6．
∵AM⊥BD，AD=10，AM=6，∴DM=
=8．
-
科目： 来源： 题型：
查看答案和解析>>【题目】求1＋2＋22＋23＋…＋22019的值，可令S＝1＋2＋22＋23＋…＋22019，则2S＝2＋22＋23＋…＋22019＋22020因此2S－S＝22020－1.仿照以上推理，计算出1＋5＋52＋53＋…＋52019的值为（ ）
A. 52019－1B. 52020－1C.
D. 
-
科目： 来源： 题型：
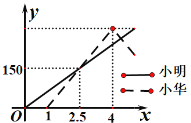
查看答案和解析>>【题目】小明和小华先后从甲地出发到乙地，小明先乘坐客车出发1小时，小华才开车前住乙地，小华到达乙地后立即按原速从乙地返回甲地。已知小明、小华离甲地距离y（千米）与小明出发时间x（小时）之间的函数关系如图所示，请根据图象解答下列问题：小华从乙地返回后再经过___小时与小明相遇.
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数填入它所属的集合内：
，0，5.2，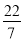 
，+（﹣4），﹣2
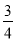，﹣（﹣3 ），0.25555…，﹣0.030030003…（1）分数集合：{______ …}
（2）非负整数集合：{______ …}
（3）有理数集合：{______ …}．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“分组合作学习”已成为推动课堂教学改革，打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析，统计图如下：
请结合图中信息解答下列问题：
（1）求出随机抽取调查的学生人数；
（2）补全分组后学生学习兴趣的条形统计图；
（3）分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，PA、PB是⊙O的切线，A、B为切点，∠APB=60°，连接PO并延长与⊙O交于C点，连接AC，BC．
（1）求证：四边形ACBP是菱形；
（2）若⊙O半径为1，求菱形ACBP的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为厉行节能减排，倡导绿色出行，今年3月以来．“共享单车”（俗称“小黄车”）公益活动登陆我市中心城区，某公司拟在甲、乙两个街道社区投放一批“小黄车”，这批自行车包括A、B两种不同款型，请回答下列问题：
问题1：单价
该公司早期在甲街区进行了试点投放，共投放A、B两型自行车各50辆，投放成本共计7500元，其中B型车的成本单价比A型车高10元，A、B两型自行车的单价各是多少？
问题2：投放方式
该公司决定采取如下投放方式：甲街区每1000人投放a辆“小黄车”，乙街区每1000人投放
辆“小黄车”，按照这种投放方式，甲街区共投放1500辆，乙街区共投放1200辆，如果两个街区共有15万人，试求a的值．
相关试题
