【题目】某校为创建“书香校园”,购置了一批图书,已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普类图书的数量与购买文学类图书的数量相等.求科普类图书平均每本的价格.
参考答案:
【答案】50
【解析】
设科普类图书平均每本的价格为x元,则文学类图书平均每本的价格为(x﹣5)元,根据数量=总价÷单价结合用10000元购买科普类图书和用9000元购买文学类图书数量相等,即可得出关于x的分式方程,解之经检验即可得出结论.
设科普类图书平均每本的价格为x元,则文学类图书平均每本的价格为(x﹣5)元,
根据题意得:![]() ,
,
解得:x=50,
经检验,x=50是所列分式方程的解,且符合题意.
答:科普类图书平均每本的价格为50元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
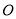 为坐标原点,点
为坐标原点,点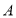 的坐标为
的坐标为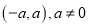 ,点
,点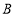 的坐标为
的坐标为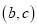 ,且
,且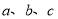 满足
满足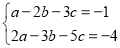 .
.(1)若
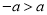 ,判断点
,判断点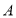 处于第几象限,给出你的结论并说明理由;
处于第几象限,给出你的结论并说明理由;(2)若
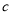 为最小正整数,
为最小正整数,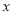 轴上是否存在一点
轴上是否存在一点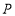 ,使三角形
,使三角形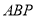 的面积等于10,若存在,求点
的面积等于10,若存在,求点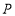 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(3)点
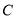 为坐标系内一点,连接
为坐标系内一点,连接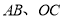 ,若
,若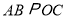 ,且
,且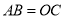 ,直接写出点
,直接写出点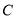 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是
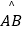 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 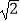 时,则阴影部分的面积为( )
时,则阴影部分的面积为( )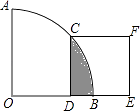
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:如图,在平面直角坐标系
 中,
中,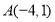 ,
, ,
,

(1)画出
 的
的 边上的高CH;
边上的高CH;(2)将
 平移到
平移到 (点
(点 和点
和点 对应,点
对应,点 和点
和点 对应,点
对应,点 和点
和点 对应),若点
对应),若点 的坐标为
的坐标为 ,请画出平移后的
,请画出平移后的 ;
;(3)若
 ,
, 为平面内一点,且满足
为平面内一点,且满足 与
与 全等,请直接写出点
全等,请直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
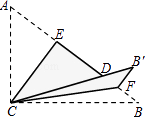
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为( )
A.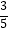
B.
C.
D.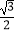
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组和不等式解应用题:
为了响应某市的“四个一”工程,培养学生的爱国主义情怀,某校学生和带队老师在5月下旬某天集体乘车去参观抗日战争纪念馆.已知学生的数量是带队老师的12倍多20人,学生和老师的总人数共540人.
(1)请求出去参观抗日战争纪念馆学生和老师各多少人?
(2)如果学校准备租赁
 型大巴车和
型大巴车和 型大巴车共14辆,(其中
型大巴车共14辆,(其中 型大巴车最多有7辆)已知
型大巴车最多有7辆)已知 型大巴车每车最多可以载35人,日租金为2000元,其中
型大巴车每车最多可以载35人,日租金为2000元,其中 型大巴车每车最多可以载45人,日租金为3000元请求出最经济的租赁车辆方案.
型大巴车每车最多可以载45人,日租金为3000元请求出最经济的租赁车辆方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的学习材料(研学问题),尝试解决问题:
(a)某学习小组在学习时遇到如下问题:如图①,在Rt△ABC中,∠C=90°,D为边BC上一点,DA=DB,E为AD延长线上一点,∠AEB=120°,猜想BC、EA、EB的数量关系,并证明结论.大家经探究发现:过点B作BF⊥AE交AE的延长线于F,如图②所示,构造全等三角形使问题容易求解,请写出解答过程.
(b)参考上述思考问题的方法,解答下列问题:
如图③,等腰△ABC中,AB=AC,H为AC上一点,在BC的延长线上顺次取点E、F,在CB的延长线上取点BD,使EF=DB,过点E作EG∥AC交DH的延长线于点G,连接AF,若∠HDF+∠F=∠BAC.
(1)探究∠BAF与∠CHG的数量关系;
(2)请在图中找出一条和线段AF相等的线段,并证明你的结论.

相关试题

