【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 ![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 ![]() 时,则阴影部分的面积为( )
时,则阴影部分的面积为( )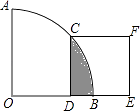
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4
参考答案:
【答案】A
【解析】解:∵在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 ![]() 的中点,
的中点,
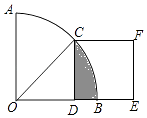
∴∠COD=45°,
∴OC= ![]() =4,
=4,
∴阴影部分的面积=扇形BOC的面积﹣三角形ODC的面积
= ![]() ×π×42﹣
×π×42﹣ ![]() ×(2
×(2 ![]() )2
)2
=2π﹣4.
所以答案是:A.
【考点精析】根据题目的已知条件,利用正方形的性质和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,过点C作CE⊥CD,且CE=CD,连接DE交BC于点F,连接BE.
(1)求证:AB⊥BE;
(2)当AD=BF时,求∠BEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:点
 不在同一条直线,
不在同一条直线, .
.(1)求证:
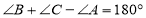 .
.(2)如图②,
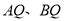 分别为
分别为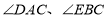 的平分线所在直线,试探究
的平分线所在直线,试探究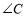 与
与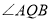 的数量关系;
的数量关系;(3)如图③,在(2)的前提下,且有
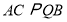 ,直线
,直线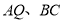 交于点
交于点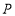 ,
,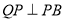 ,请直接写出
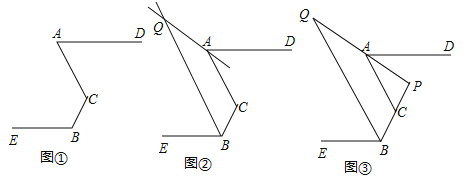
,请直接写出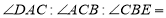 ______________.
______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
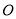 为坐标原点,点
为坐标原点,点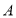 的坐标为
的坐标为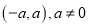 ,点
,点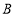 的坐标为
的坐标为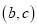 ,且
,且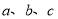 满足
满足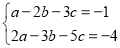 .
.(1)若
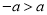 ,判断点
,判断点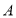 处于第几象限,给出你的结论并说明理由;
处于第几象限,给出你的结论并说明理由;(2)若
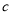 为最小正整数,
为最小正整数,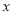 轴上是否存在一点
轴上是否存在一点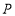 ,使三角形
,使三角形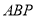 的面积等于10,若存在,求点
的面积等于10,若存在,求点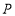 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(3)点
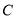 为坐标系内一点,连接
为坐标系内一点,连接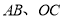 ,若
,若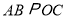 ,且
,且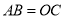 ,直接写出点
,直接写出点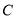 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:如图,在平面直角坐标系
 中,
中,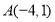 ,
, ,
,

(1)画出
 的
的 边上的高CH;
边上的高CH;(2)将
 平移到
平移到 (点
(点 和点
和点 对应,点
对应,点 和点
和点 对应,点
对应,点 和点
和点 对应),若点
对应),若点 的坐标为
的坐标为 ,请画出平移后的
,请画出平移后的 ;
;(3)若
 ,
, 为平面内一点,且满足
为平面内一点,且满足 与
与 全等,请直接写出点
全等,请直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为创建“书香校园”,购置了一批图书,已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普类图书的数量与购买文学类图书的数量相等.求科普类图书平均每本的价格.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为( )
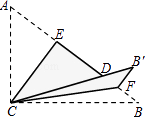
A.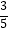
B.
C.
D.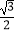
相关试题

