【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
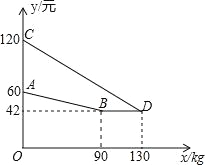
(1)求线段AB所表示的y1与x之间的函数表达式;线段CD所表示的y2与x之间的函数表达式.
(2)当该产品产量为多少时,获得的利润最大?最大利润是多少?
参考答案:
【答案】(1)y1=-0.2x+60(0≤x≤90);y2=-0.6x+120(0≤x≤130);(2)当该产品产量为75kg时,获得的利润最大,最大值为2250.
【解析】
试题分析:(1)根据线段AB、线段CD经过的两点的坐标利用待定系数法确定一次函数的表达式即可;
(3)利用:总利润=每千克利润×产量,根据x的取值范围列出有关x的二次函数,求得最值比较可得.
试题解析:(1)设线段AB所表示的y1与x之间的函数关系式为y1=k1x+b1,
∵y1=k1x+b1的图象过点(0,60)与(90,42),
∴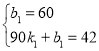
∴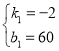 ,
,
∴段AB所表示的一次函数的表达式为;y1=-0.2x+60(0≤x≤90);
设y2与x之间的函数关系式为y2=k2x+b2,
∵经过点(0,120)与(130,42),
∴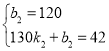 ,
,
解得: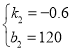 ,
,
∴线段CD所表示的一次函数的表达式为y2=-0.6x+120(0≤x≤130);
(2)设产量为xkg时,获得的利润为W元,
①当0≤x≤90时,W=x[(-0.6x+120)-(-0.2x+60)]=-0.4(x-75)2+2250,
∴当x=75时,W的值最大,最大值为2250;
②当90≤x≤130时,W=x[(-0.6x+120)-42]=-0.6(x-65)2+2535,
∴当x=90时,W=-0.6(90-65)2+2535=2160,
由-0.6<0知,当x>65时,W随x的增大而减小,
∴90≤x≤130时,W≤2160,
因此当该产品产量为75kg时,获得的利润最大,最大值为2250.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(a+2)2+4|b-5|=0,求(7a+8b)-(-4a+6b)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系
 的原点O在格点上,
的原点O在格点上,  轴、
轴、 轴都在网格线上.线段AB的端点A、B在格点上.
轴都在网格线上.线段AB的端点A、B在格点上.
(1)将线段AB绕点O逆时针90°得到线段A1B1,请在图中画出线段A1B1;
(2)在(1)的条件下,线段A2B2与线段A1B1关于原点O成中心对称,请在图中画出线段A2B2;
(3)在(1)、(2)的条件下,点P是此平面直角坐标系内的一点,当以点A、B、B2、P为顶点的四边形是平行四边形时,请直接写出点P的坐标: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家新开发的一种电动车如图,它的大灯A射出的光线AB,AC与地面MN所夹的锐角分别为8°和10°,大灯A与地面离地面的距离为1m求该车大灯照亮地面的宽度BC.(不考虑其它因素)(参数数据:sin8°=
 ,tan8°=
,tan8°=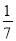 ,sin10°=
,sin10°= ,tan10°=
,tan10°= )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】要用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”,首先应假设_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一多项式除以2x2-3,得到的商式为x+4,余式为3x+2,则此多项式为
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(21x4y3-35x3y2+7x2y2)÷(-7x2y).
相关试题

