搜索
【题目】要用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”，首先应假设_____．
参考答案：
【答案】每一个角都小于45°
【解析】
试题反证法的第一步是假设命题的结论不成立，据此可以得到答案．
若用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”时，应假设每一个角都小于45°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形网格中，每个小正方形的边长为1个单位长度．平面直角坐标系
的原点O在格点上，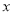 
轴、
轴都在网格线上．线段AB的端点A、B在格点上．
（1）将线段AB绕点O逆时针90°得到线段A1B1，请在图中画出线段A1B1；
（2）在（1）的条件下，线段A2B2与线段A1B1关于原点O成中心对称，请在图中画出线段A2B2；
（3）在（1）、（2）的条件下，点P是此平面直角坐标系内的一点，当以点A、B、B2、P为顶点的四边形是平行四边形时，请直接写出点P的坐标： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某厂家新开发的一种电动车如图，它的大灯A射出的光线AB，AC与地面MN所夹的锐角分别为8°和10°，大灯A与地面离地面的距离为1m求该车大灯照亮地面的宽度BC．（不考虑其它因素）（参数数据：sin8°=
，tan8°=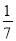
，sin10°=
，tan10°=
）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某企业生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1（单位：元）、销售价y2（单位：元）与产量x（单位：kg）之间的函数关系．
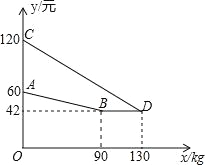
（1）求线段AB所表示的y1与x之间的函数表达式；线段CD所表示的y2与x之间的函数表达式．
（2）当该产品产量为多少时，获得的利润最大？最大利润是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一多项式除以2x2-3，得到的商式为x+4，余式为3x+2，则此多项式为
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：（21x4y3-35x3y2+7x2y2）÷（-7x2y）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）问题情境：如图1，在正方形ABCD中，E、F、G、H分别为AB，BC，CD，DA边上的动点，连接EG，HF相交于点O，且∠HOE=∠ADC．试探究：EG与FH的数量关系，并说明理由．
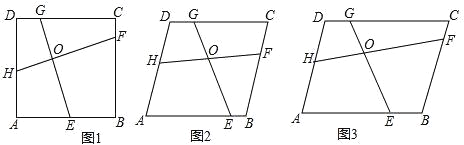
（2）拓展延伸：如图2，在菱形ABCD中，E、F、G、H分别为AB，BC，CD，DA边上的动点，连接EG，HF相交于点O，且∠HOE=∠ADC，试探究：（1）中EG与FH的数量关系还成立吗？并说明理由．
（3）反思提升：若将（2）中的菱形ABCD改为平行四边形ABCD（如图3），AB=a，AD=b，其他条件不变，则
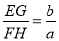的猜想正确吗？请说明理由．
相关试题
