【题目】某厂家新开发的一种电动车如图,它的大灯A射出的光线AB,AC与地面MN所夹的锐角分别为8°和10°,大灯A与地面离地面的距离为1m求该车大灯照亮地面的宽度BC.(不考虑其它因素)(参数数据:sin8°=![]() ,tan8°=
,tan8°=![]() ,sin10°=
,sin10°=![]() ,tan10°=
,tan10°=![]() )
)

参考答案:
【答案】该车大灯照亮地面的宽度BC是1.4m.
【解析】
试题分析:通过构造直角三角形来解答,过A作AD⊥MN于D,就有了∠ABN、∠ACN的度数,又已知AE的长,可在直角三角形ABE、ACE中分别求出BE、CE的长,BC就能求出.
试题解析:如图,

过A作AD⊥MN于点D,
在Rt△ACD中,tan∠ACD=![]() ,CD=5.6(m),
,CD=5.6(m),
在Rt△ABD中,tan∠ABD=![]() ,BD=7(m),
,BD=7(m),
则BC=7-5.6=1.4(m).
答:该车大灯照亮地面的宽度BC是1.4m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“6·26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作了频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段(
 表示分数)
表示分数)频数
频率
50≤
 <60
<604
0.1
60≤
 <70
<70
0.2
70≤
 <80
<8012

80≤
 <90
<9010
0.25
90≤
 <100
<1006
0.15

(1)表中
 = ,
= ,  = ,并补全直方图;
= ,并补全直方图;(2)若用扇形统计图描述此成绩统计分布情况,则分数段80≤
 <100对应扇形的圆心角度数是 ;
<100对应扇形的圆心角度数是 ;(3)请估计该年级分数在60≤
 <70的学生有多少人?
<70的学生有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】(a+2)2+4|b-5|=0,求(7a+8b)-(-4a+6b)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系
 的原点O在格点上,
的原点O在格点上,  轴、
轴、 轴都在网格线上.线段AB的端点A、B在格点上.
轴都在网格线上.线段AB的端点A、B在格点上.
(1)将线段AB绕点O逆时针90°得到线段A1B1,请在图中画出线段A1B1;
(2)在(1)的条件下,线段A2B2与线段A1B1关于原点O成中心对称,请在图中画出线段A2B2;
(3)在(1)、(2)的条件下,点P是此平面直角坐标系内的一点,当以点A、B、B2、P为顶点的四边形是平行四边形时,请直接写出点P的坐标: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
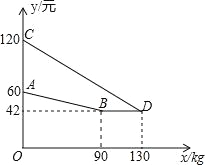
(1)求线段AB所表示的y1与x之间的函数表达式;线段CD所表示的y2与x之间的函数表达式.
(2)当该产品产量为多少时,获得的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】要用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”,首先应假设_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一多项式除以2x2-3,得到的商式为x+4,余式为3x+2,则此多项式为
相关试题

