【题目】如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,﹣4)
(1)求出图象与x轴的交点A、B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=![]() S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)A(﹣1,0),B(3,0);(2)存在合适的点P,坐标为(4,5)或(﹣2,5).
【解析】试题分析:
(1)由二次函数y=(x+m)2+k的顶点坐标为M(1,﹣4)可得解析式为: ![]() ,解方程:
,解方程: ![]() 可得点A、B的坐标;
可得点A、B的坐标;
(2)设点P的纵坐标为![]() ,由△PAB与△MAB同底,且S△PAB=
,由△PAB与△MAB同底,且S△PAB=![]() S△MAB,可得:
S△MAB,可得: ![]() ,从而可得
,从而可得![]() =
=![]() ,结合点P在抛物线
,结合点P在抛物线![]() 的图象上,可得
的图象上,可得![]() =5,由此得到:
=5,由此得到: ![]() ,解方程即可得到点P的坐标.
,解方程即可得到点P的坐标.
试题解析:
(1)∵抛物线解析式为y=(x+m)2+k的顶点为M(1,﹣4)
∴![]() ,
,
当y=0时,(x﹣1)2﹣4=0,解得x1=3,x2=﹣1,
∴A(﹣1,0),B(3,0);
(2)∵△PAB与△MAB同底,且S△PAB=![]() S△MAB,
S△MAB,
∴![]() ,即
,即![]() =
=![]() ,
,
又∵点P在y=(x﹣1)2﹣4的图象上,
∴yP≥﹣4,
∴![]() =5,则
=5,则![]() ,解得:
,解得: ![]() ,
,
∴存在合适的点P,坐标为(4,5)或(﹣2,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面内点M(x,y),若x,y满足下列条件,请说出点M的位置.
(1)xy<0;(2)x+y=0;(3)
 =0.
=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.不正确的有( )
A.①②B.②③C.②④D.④③
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中:①﹣|﹣1|②﹣{﹣[﹣(﹣2)]},③(﹣2)3,④﹣22,⑤﹣(4)3,其运算结果为正数的个数有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,四边形ABCD的四个顶点的坐标分别为A(0,0)、B(9,0)、C(7,5)、D(2,7).
(1)试计算四边形ABCD的面积;
(2)若将该四边形各顶点的横坐标都加2,纵坐标都加3,其面积怎么变化?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+3)2与|y﹣2|互为相反数,则xy的值为( )
A.9B.﹣9C.8D.﹣8
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线
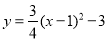 .
.(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
相关试题

