【题目】在平面直角坐标系xOy中,函数y= ![]() (k1>0,x>0)、函数y=
(k1>0,x>0)、函数y= ![]() (k2<0,x<0)的图象分别经过OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
(k2<0,x<0)的图象分别经过OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( ) 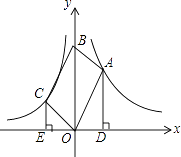
A.4:9
B.2:3
C.3:2
D.9:4
参考答案:
【答案】D
【解析】解:作AF⊥OB于F,如图所示:
则∠AFB=∠OEC=∠ADO=90°,AF=OD,CE∥OB,
∴∠OCE=∠BOC,
∵四边形OABC是平行四边形,
∴OC=AB,OC∥AB,
∴∠ABF=∠BOC,
∴∠ABF=∠OCE,
在△ABF和△OCE中,
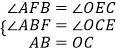 ,
,
∴△ABF≌△OCE(AAS),
∴AF=OE,
∴OD=OE,
∵△AOD的面积= ![]() ADOD=
ADOD= ![]() k1,△OCE的面积=
k1,△OCE的面积= ![]() CEOE=
CEOE= ![]() |k2|,|k1|:|k2|=9:4,
|k2|,|k1|:|k2|=9:4,
∴ ![]() =
= ![]() =
= ![]() .
.
故选:D.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.
现有点A(2,0)和抛物线E上的点B(-1,n),请完成下列任务:
(1)【尝试】
①当t=2时,抛物线E的顶点坐标是.
②点A抛物线E上;(填“在”或“不在”),
③n=.
(2)【发现】通过②和③的演算可知,对于t取任何不为零的实数,抛物线E总过定点,这个定点的坐标是.
(3)【应用1】二次函数y=-3x2+5x+2是二次函数y=x2-3x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
(4)【应用2】以AB为一边作矩形ABCD,使得其中一个顶点落在y轴上,若抛物线E经过点A、B、C,求出所有符合条件的t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
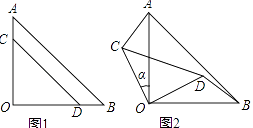
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.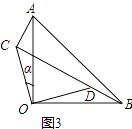
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
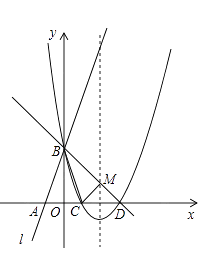
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,A,B在数轴上对应的数分别用a,b表示,且(
 ab+100)2+|a-20|=0, P是数轴上的一个动点.
ab+100)2+|a-20|=0, P是数轴上的一个动点.(1)在数轴上标出A、B的位置,并求出A、B之间的距离.
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数.
(3)动点M从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7 个单位长度,…,点M能移动到与A或B重合的位置吗?若都不能,请直接回答,若能,请直接指出,第几次移动与哪一点重合.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次期中考试中,甲、乙、丙、丁、戊五位同学的数学、英语成绩等有关信息如下表所示(单位:分):
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式:标准分=(个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好,请问甲同学在本次考试中,数学与英语哪个学科考得更好?
甲
乙
丙
丁
戊
平均分
标准差
数学
71
72
69
68
70
英语
88
82
94
85
76
85
-
科目: 来源: 题型:
查看答案和解析>>【题目】读句画图:如图,直线CD与直线AB相交于C,
根据下列语句画图:
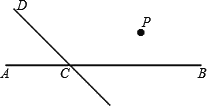
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.
相关试题

