【题目】如图,点![]() 是直角三角形
是直角三角形![]() 斜边
斜边![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() ,分别过点
,分别过点![]() ,
,![]() 向直线
向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 的中点.
的中点.
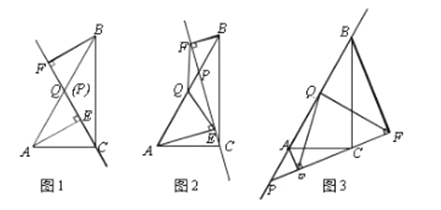
(1)如图1,当点![]() 与点
与点![]() 重合时,
重合时,![]() 与
与![]() 的位置关系是______,
的位置关系是______,![]() 与
与![]() 的数量关系是______;
的数量关系是______;
(2)如图2,当点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 重合)时,试猜想
重合)时,试猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,此时(2)中的结论是否仍成立?请说明理由.
的延长线上时,此时(2)中的结论是否仍成立?请说明理由.
参考答案:
【答案】(1)AE∥BF,QE=QF,(2)QE=QF,证明见解析;(3)当点P在线段BA(或AB)的延长线上时,此时(2)中的结论成立,证明见解析.
【解析】
(1)根据AAS推出△AEQ≌△BFQ即可得出答案;
(2)延长EQ交BF于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可;
(3)延长EQ交FB于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可
(1)如图1,
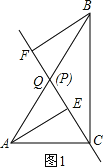
当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是AE=BF,
理由:
∵Q为AB的中点,
∴AQ=BQ,
∵AE⊥CQ,BF⊥CQ,
∴AE∥BF,∠AEQ=∠BFQ=90°,
在△AEQ和△BFQ中
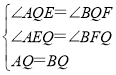
∴△AEQ≌△BFQ(AAS),
∴QE=QF,
(2)
QE=QF,
证明:如图2,延长EQ交BF于D,
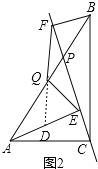
∵由(1)知:AE∥BF,
∴∠AEQ=∠BDQ,
在△AEQ和△BDQ中
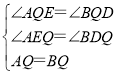
∴△AEQ≌△BDQ(AAS),
∴EQ=DQ,
∵∠BFE=90°,
∴QE=QF;
(3)当点P在线段BA(或AB)的延长线上时,此时(2)中的结论成立,
证明:延长EQ交FB于D,如图3,
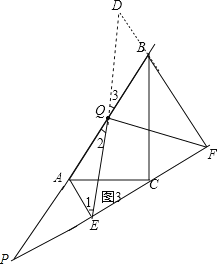
∵由(1)知:AE∥BF,
∴∠AEQ=∠BDQ,
在△AEQ和△BDQ中
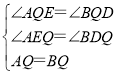
∴△AEQ≌△BDQ(AAS),
∴EQ=DQ,
∵∠BFE=90°,
∴QE=QF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为直线
为直线 上一点,
上一点, 平分
平分 ,则以下结论正确的有______.(只填序号)①
,则以下结论正确的有______.(只填序号)① 与
与 互为余角;②若
互为余角;②若 ,则
,则 ;③
;③ ;④
;④ 平分
平分 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校七年级学生对
 (极限挑战);
(极限挑战);  (奔跑吧),
(奔跑吧), (王牌对王牌);
(王牌对王牌);  (向往的生活)四个点数节目的喜爱情况,某调查组从该校七年级学生中随机抽取了位
(向往的生活)四个点数节目的喜爱情况,某调查组从该校七年级学生中随机抽取了位 学生进行调查统计(要求每位选出并且只能选一个自己喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2).根据以上信息,回答下列问题:
学生进行调查统计(要求每位选出并且只能选一个自己喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2).根据以上信息,回答下列问题:(1)
 _____________,
_____________, ________________;
________________;(2)在图1中,喜爱(奔跑吧)节目所对应的扇形的圆心角的度数是___________;
(3)请根据以上信息补全图2的条形统计图;
(4)已知该校七年级共有540名学生,那么他们当中最喜爱(王牌对王牌)这个节目的学生有多少人?


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,等边△ABC中,D、E分别在BC、AC边上运动,且始终保持BD=CE,点D、E始终不与等边△ABC的顶点重合.连接AD、BE,AD、BE交于点F.
(1)写出在运动过程中始终全等的三角形,井选择其中一组证明;
(2)运动过程中,∠BFD的度数是否会改变?如果改变,请说明理由;如果不变,求出∠BFD的度数,再说明理由.
(3)直接写出运动过程中,AE、AB、BD三条线段长度之间的等量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.
如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.
若△ABC经γ(1,180°)变换后得△A1B1C1,△A1B1C1经γ(2,180°)变换后得△A2B2C2,△A2B2C2经γ(3,180°)变换后得△A3B3C3,依此类推……
△An﹣1Bn﹣1Cn﹣1经γ(n,180°)变换后得△AnBnCn,则点A1的坐标是__,点A2018的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明到小陈家所在的美丽乡村游玩,在村头A处小明接到小陈发来的定位,发现小陈家C在自己的北偏东45°方向,于是沿河边笔直的绿道l步行200米到达B处,这时定位显示小陈家C在自己的北偏东30°方向,如图所示,根据以上信息和下面的对话,请你帮小明算一算他还需沿绿道继续直走多少米才能到达桥头D处(精确到1米)(备用数据:
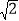 ≈1.414,
≈1.414,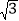 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】蚌埠云轨测试线自开工以来备受关注,据了解我市首期工程云轨线路约12千米,若该任务由甲、乙两工程队先后接力完成,甲工程队每天修建
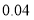 千米,乙工程队每天修建
千米,乙工程队每天修建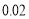 千米,两工程队共需修建500天,求甲、乙两工程队分别修建云轨多少千米?
千米,两工程队共需修建500天,求甲、乙两工程队分别修建云轨多少千米?根据题意,小刚同学列出了一个尚不完整的方程组:
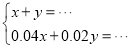
(1)根据小刚同学所列的方程组,请你分别指出未知数
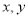 表示的意义.
表示的意义.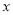 表示____________;
表示____________;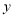 表示________________.
表示________________.(2)小红同学“设甲工程队修建云轨
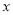 千米,乙工程队修建云轨
千米,乙工程队修建云轨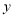 千米”请你利用小红同学设的未知数解决问题.
千米”请你利用小红同学设的未知数解决问题.
相关试题

