【题目】为了解某校七年级学生对![]() (极限挑战);
(极限挑战); ![]() (奔跑吧),
(奔跑吧),![]() (王牌对王牌);
(王牌对王牌); ![]() (向往的生活)四个点数节目的喜爱情况,某调查组从该校七年级学生中随机抽取了位
(向往的生活)四个点数节目的喜爱情况,某调查组从该校七年级学生中随机抽取了位![]() 学生进行调查统计(要求每位选出并且只能选一个自己喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2).根据以上信息,回答下列问题:
学生进行调查统计(要求每位选出并且只能选一个自己喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2).根据以上信息,回答下列问题:
(1)![]() _____________,
_____________,![]() ________________;
________________;
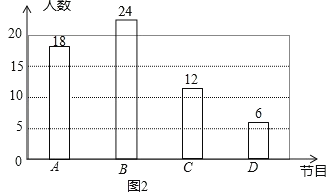
(2)在图1中,喜爱(奔跑吧)节目所对应的扇形的圆心角的度数是___________;
(3)请根据以上信息补全图2的条形统计图;
(4)已知该校七年级共有540名学生,那么他们当中最喜爱(王牌对王牌)这个节目的学生有多少人?


参考答案:
【答案】(1)![]() ;(2)144°;(3)见解析;(4)他们喜欢(王牌对王牌)这个节目的学生约有108人.
;(2)144°;(3)见解析;(4)他们喜欢(王牌对王牌)这个节目的学生约有108人.
【解析】
(1)从两个统计图中可以得到“D《向往的生活》”有6人,占调查人数的10%,可求出调查人数,即m的值,进而可求出“B”的人数,计算出“C”组所占的百分比;
(2)“B”组占40%,因此圆心角占360°的40%;
(3)补齐“B”组的条形即可;
(4)C组占调查人数的![]() ,因此估计总体中,540人的
,因此估计总体中,540人的![]() 喜欢《王牌对王牌》节目.
喜欢《王牌对王牌》节目.
(1)m=6÷10%=60,B的人数为:60×40%=24人,12÷60=20%,因此n=20.
故答案为:60,20.
(2)360°×40%=144°.
故答案为:144°;
(3)补全条形统计图如图所示:
(4)540![]() 108人,
108人,
答:他们当中最喜欢《王牌对王牌》这个节目的学生有108人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为直线x=
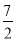 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
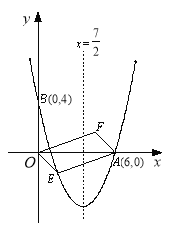
查看答案和解析>>【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A. 3cm B.
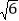 cm C. 2.5cm D.
cm C. 2.5cm D. 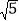 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为直线
为直线 上一点,
上一点, 平分
平分 ,则以下结论正确的有______.(只填序号)①
,则以下结论正确的有______.(只填序号)① 与
与 互为余角;②若
互为余角;②若 ,则
,则 ;③
;③ ;④
;④ 平分
平分 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,等边△ABC中,D、E分别在BC、AC边上运动,且始终保持BD=CE,点D、E始终不与等边△ABC的顶点重合.连接AD、BE,AD、BE交于点F.
(1)写出在运动过程中始终全等的三角形,井选择其中一组证明;
(2)运动过程中,∠BFD的度数是否会改变?如果改变,请说明理由;如果不变,求出∠BFD的度数,再说明理由.
(3)直接写出运动过程中,AE、AB、BD三条线段长度之间的等量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是直角三角形
是直角三角形 斜边
斜边 上一动点(不与点
上一动点(不与点 ,
, 重合),作直线
重合),作直线 ,分别过点
,分别过点 ,
, 向直线
向直线 作垂线,垂足分别为
作垂线,垂足分别为 ,
,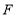 ,
,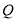 为斜边
为斜边 的中点.
的中点.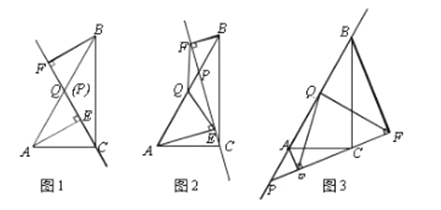
(1)如图1,当点
 与点
与点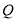 重合时,
重合时,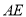 与
与 的位置关系是______,
的位置关系是______, 与
与 的数量关系是______;
的数量关系是______;(2)如图2,当点
 在线段
在线段 上(不与点
上(不与点 重合)时,试猜想
重合)时,试猜想 与
与 的数量关系,并说明理由;
的数量关系,并说明理由;(3)如图3,当点
 在线段
在线段 的延长线上时,此时(2)中的结论是否仍成立?请说明理由.
的延长线上时,此时(2)中的结论是否仍成立?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.
如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.
若△ABC经γ(1,180°)变换后得△A1B1C1,△A1B1C1经γ(2,180°)变换后得△A2B2C2,△A2B2C2经γ(3,180°)变换后得△A3B3C3,依此类推……
△An﹣1Bn﹣1Cn﹣1经γ(n,180°)变换后得△AnBnCn,则点A1的坐标是__,点A2018的坐标是 .

相关试题

