【题目】在等腰△ABC中,三边分别为a,b,c,其中a=5,若关于x的方程x2+(b﹣2)x+b﹣3=0有两个相等的实数根,求△ABC的周长.
参考答案:
【答案】△ABC的周长是13或14.
【解析】试题分析:由方程有两个相等的实数根可得到关于b的方程,可求得b的值,再分a为底和a为腰两种情况分别求其周长即可.
试题解析:∵方程x2+(b-2)x+b-3=0有两个相等的实数根,
∴△=0,即(b-2)2-4(b-3)=0,解得b1=b2=4,
①当a为底,b为腰时,能构成三角形,周长为4+4+5=13,
②当b为底,a为腰时,也能构成三角形,周长为=4+5+5=14,
∴△ABC的周长是13或14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把半径为4cm的半圆围成一个圆锥,则圆锥的底面圆半径为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. x4x4=x16 B. (a3)2a4=a9
C. (ab2)3÷(﹣ab)2=﹣ab4 D. (a6)2÷(a4)3=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2b-2c)2等于_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x2﹣4=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;(2)将△A1B1C1沿x轴方向向左平移3个单位、再沿
 轴向下平移1个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
轴向下平移1个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
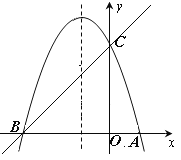
(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标;(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
相关试题

