【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
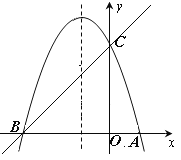
(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;
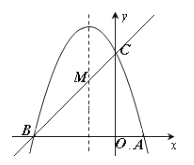
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标;(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)M(-1,2);(3)满足条件的点P共有四个,分别为
;(2)M(-1,2);(3)满足条件的点P共有四个,分别为![]() (-1,-2),
(-1,-2), ![]() (-1,4),
(-1,4), ![]() (-1,
(-1,![]() ) ,
) ,![]() (-1,
(-1,![]() ).
).
【解析】
试题分析:(1)已知抛物线y=ax2+bx+c的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,可得方程组,解方程组可求得a、b、c的值,即可得抛物线的解析式;根据抛物线的对称性和点A的坐标(1,0)可求得B点的坐标(-3,0),用待定系数法可求得直线BC的解析式;(2)使MA+MC最小的点M应为直线BC与对称轴x=-1的交点,把x=-1代入直线BC的解析式求得y的值,即可得点M的坐标;(3)分①B为直角顶点,②C为直角顶点,③P为直角顶点三种情况分别求点P的坐标.
试题解析:(1)依题意,得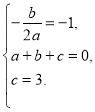 解之,得
解之,得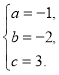
∴抛物线解析式为![]() .
.
∵对称轴为x=-1,且抛物线经过A(1,0),
∴B(-3,0).
把B(-3,0)、C(0,3)分别直线y=mx+n,得
![]() 解之,得
解之,得![]()
∴直线BC的解析式为![]() .
.
(2)∵MA=MB,∴MA+MC=MB+MC.
∴使MA+MC最小的点M应为直线BC与对称轴x=-1的交点.
设直线BC与对称轴x=-1的交点为M,把x=-1
代入直线![]() ,得y=2.
,得y=2.
∴M(-1,2)
(3)设P(-1,t),结合B(-3,0),C(0, 3),得BC2=18,
PB2=(-1+3)2+t2=4+t2,
PC2=(-1)2+(t-3)2=t2-6t+10.
①若B为直角顶点,则BC2+PB2=PC2,即18+4+t2=t2-6t+10.
解之,得t=-2.
②若C为直角顶点,则BC2+PC2=PB2,即
18+t2-6t+10=4+t2.解之,得t=4.
③若P为直角顶点,则PB2+PC2=BC2,即
4+t2+t2-6t+10=18.解之,得t1=![]() ,t2=
,t2=![]() .
.
综上所述,满足条件的点P共有四个,分别为![]() (-1,-2),
(-1,-2), ![]() (-1,4),
(-1,4), ![]() (-1,
(-1,![]() ) ,
) ,![]() (-1,
(-1,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,三边分别为a,b,c,其中a=5,若关于x的方程x2+(b﹣2)x+b﹣3=0有两个相等的实数根,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x2﹣4=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;(2)将△A1B1C1沿x轴方向向左平移3个单位、再沿
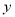 轴向下平移1个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
轴向下平移1个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】宇宙现在的年龄约为200亿年,200亿用科学记数法表示为( )
A. 0.2×1011 B. 2×1010 C. 200×108 D. 2×109
-
科目: 来源: 题型:
查看答案和解析>>【题目】11.497精确到百分位约是11.50。(_____)
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式1﹣2x≥3的解是_____.
相关试题

