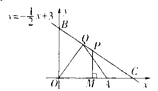
【题目】如图，点A的坐标为(4，0)．点P是直线y= x+3在第一象限内的点，过P作PMx轴于点M，O是原点．

(1)设点P的坐标为(x, y)，试用它的纵坐标y表示△OPA的面积S；

(2)S与y是怎样的函数关系?它的自变量y的取值范围是什么?

(3)如果用P的坐标表示△OPA的面积S，S与x是怎样的函数关系?它的自变量的取值范围是什么?

(4)在直线y= x+3上求一点Q，使△QOA是以OA为底的等腰三角形．

参考答案：

【答案】(1)S=2y．(2) S是y的正比例函数，自变量y的取值范围是0<y<3．(3) Sx+6，S是x的一次函数，自变量的取值范围是0<x<6．(4) 点Q的坐标为( 2，2)．

【解析】试题分析：（1）先求OA长，再找P点的纵坐标，计算面积.

（2）利用函数定义知，是正比例函数,范围根据图象可知.

（3）由（1）可知，可得到S是x的函数关系.

（4）△QOA是以OA为底的等腰三角形,所以可知Q点的横坐标是2，再代入一次函数可知P点坐标.

试题解析：

(1)直线y= x+3与)与y轴的交点为B(0，3)，设点P(x，y)，因为点P在第一象限，x>0，y>0，所以S=OA·PM=×y×4=2y．

(2)S是y的正比例函数，自变量y的取值范围是0<y<3．

(3)S=2y=2(x+3)= x+6，S是x的一次函数，自变量的取值范围是0<x<6．

(4)因为△QOA是以OA为底的等腰三角形，所以点Q在OA的中垂线上，

设Q (x0, y0) 则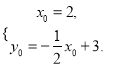 解得 点Q的坐标为( 2，2)．

关闭