Question

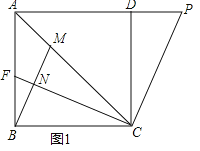
【题目】如图1，在正方形ABCD中，点P为AD延长线上一点，连接AC、CP，过点C作CF⊥CP交于C，交AB于点F，过点B作BM⊥CF于点N，交AC于点M．

（1）若AP=AC，BC=4，求S△ACP；

（2）若CP﹣BM=2FN，求证：BC=MC；

Answer 1

【答案】（1）S△ACP=7；（2）证明见解析.

【解析】试题分析：（1）由正方形的性质得出AB=BC=CD=4，∠ADC=∠CDP=∠ABC=∠BCD=90°，由勾股定理求出AC，得出AP，即可求出S△ACP；（2）在CF上截取NG=FN，连接BG，则CF-CG=2FN，证出∠BCF=∠DCP，由ASA证明△BCF≌△DCP，得出CF=CP，证出CG=BM，由SAS证明△ABM≌△BCG，得出∠AMB=∠BGC，因此∠BMC=∠BGF，由线段垂直平分线的性质得出BF=BG，得出∠BFG=∠BGF，因此∠BMC=∠CBM，即可得出结论

试题解析：（1）∵四边形ABC是正方形，

∴AD∥BC，AB=BC=CD=4，∠ADC=∠CDP=∠ABC=∠BCD=90°，

∴AC=，

∴AP=AC=×=，

∴S△ACP=AP×CD=××4=7；

（2）证明：在CF上截取NG=FN，连接BG，如图1所示：

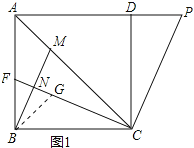
则CF﹣CG=2FN，

∵CF⊥CP，

∴∠PCF=90°，

∴∠BCF=∠DCP，

在△BCF和△DCP中， ，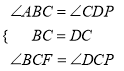

∴△BCF≌△DCP（ASA），

∴CF=CP，

∵CP﹣BM=2FN，

∴CG=BM，

∵∠ABC=90°，BM⊥CF，

∴∠ABM=∠BCG，∠BFG=∠CBM，

在△ABM和△BCG中， ，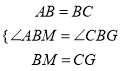

∴△ABM≌△BCG（SAS），

∴∠AMB=∠BGC，

∴∠BMC=∠BGF，

∵GN=FN，BM⊥CF，

∴BF=BG，

∴∠BFG=∠BGF，

∴∠BMC=∠CBM，

∴BC=MC.