【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.

参考答案:
【答案】(1)AB=DE,AB⊥DE.理由见解析;(2)证明见解析.
【解析】试题分析:(1)根据垂直的定义可证得∠DAE=∠ACB=90°,然后根据ASA可证△ABC≌△DEA,从而得证AB=DE,且∠3=∠1,然后根据直角三角形的内角和等量代换可证得AB⊥DE;
(2)根据三角形的面积和四边形的面积,可知S四边形ADBE= S△ADE+ S△BDE,S四边形ADBE=S△ABE+S△ADB=![]() a2+
a2+![]() b2可得证符合勾股定理的逆定理.
b2可得证符合勾股定理的逆定理.
试题解析:(1)解:AB=DE, AB⊥DE.
如图2,∵AD⊥CA,∴∠DAE=∠ACB=90°,
∵AE=BC,∠DAE=∠ACB,AD=AC,∴△ABC≌△DEA,∴AB=DE,
∠3=∠1,∵∠DAE=90°,∴∠1+∠2=90°,∴∠3+∠2=90°,
∴∠AFE=90°,∴AB⊥DE.
(2)如图2,∵S四边形ADBE= S△ADE+ S△BDE=![]() DE·AF+
DE·AF+![]() DE·BF=
DE·BF=![]() DE·AB =
DE·AB =![]() c2,
c2,
S四边形ADBE=S△ABE+S△ADB=![]() a2+
a2+![]() b2,
b2,
∴![]() a2+
a2+![]() b2=
b2=![]() c2,∴a2+b2=c2.
c2,∴a2+b2=c2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=5,cos∠ABC=
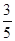 ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
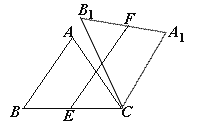
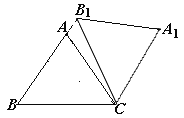
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮的体重为43.90kg,精确到1kg得到的近似数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(a﹣3)x|a﹣1|+x﹣1=0是一元二次方程,则a的值是( )
A. ﹣1B. 2C. ﹣1或3D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:9x2y﹣6xy+y=_____.
-
科目: 来源: 题型:
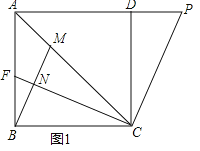
查看答案和解析>>【题目】如图1,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,过点C作CF⊥CP交于C,交AB于点F,过点B作BM⊥CF于点N,交AC于点M.
(1)若AP=
 AC,BC=4,求S△ACP;
AC,BC=4,求S△ACP;(2)若CP﹣BM=2FN,求证:BC=MC;
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016湖北襄阳第25题)
如图,已知点A的坐标为(-2,0),直线y=-
 +3与x轴,y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A,B,C三点.
+3与x轴,y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A,B,C三点.(1)请直接写出B,C两点的坐标,抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P为第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F若四边形DEFP为平行四边形,求点P的坐标;
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N点.Q从点B出发,以每秒l个单位长度的速度沿线段BA向点A运动,运动时间为t(秒).当t(秒)为何值时,存在QMN为等腰直角三角形?

相关试题

