【题目】某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:

(1)求出表中a,b,c的数值,并补全频数分布直方图;
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分.
参考答案:
【答案】(1)a=40,b=0.4,c=0.3,补图见解析;(2)中位数落在85≤x<90这一段.(3)平均分: 89分.
【解析】试题分析:分数在95x<100之间的人数÷频率得到总人数,a=总人数×0.2,b=80÷总人数,c=60÷总人数,根据计算结果补全统计图即可;(2)根据中位数的定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数。如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,结合统计图可得答案.(3)根据求平均数公式计算即可.
试题解析:(1)20÷0.1=200,a=200×0.2=40;b=80÷200=0.4;c=60÷200=0.3.
统计图如图:

(2)把所用数据从小到大排列,位置处于中间的是第100名和101名,由统计图可以看出第100名和101名成绩落在8590分数段;
(3)(82.5×40+87.5×80+92.5×60+97.5×20)÷200=89
答:平均分为89分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的多项式(x2+x-n)(mx-3)的展开式中不含x2和常数项,求m,n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程
 ﹣8=﹣
﹣8=﹣  的解与方程4x﹣(3a+1)=6x+2a﹣1的解相同,求式子a﹣a2的值.
的解与方程4x﹣(3a+1)=6x+2a﹣1的解相同,求式子a﹣a2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在已知线段AB的同侧构造∠FAB=∠GBA,并且在射线AF,BG上分别取点D和E,在线段AB上取点C,连结DC和EC.

(1)如图,若AD=3,BE=1,△ADC≌△BCE.在∠FAB=∠GBA=60或∠FAB=∠GBA=90两种情况中任选一种,解决以下问题:
①线段AB的长度是否发生变化,直接写出长度或变化范围;
②∠DCE的度数是否发生变化,直接写出度数或变化范围.
(2)若AD=a,BE=b,∠FAB=∠GBA=α,且△ADC和△BCE这两个三角形全等,请求出:
①线段AB的长度或取值范围,并说明理由;
②∠DCE的度数或取值范围,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B,顶点为C,将抛物线在A,C,B之间的部分记为图象E(A,B两点除外).
(1)求抛物线的顶点坐标.
(2)AB=6时,经过点C的直线y=kx+b(k≠0)与图象E有两个交点,结合函数的图象,求k的取值范围.
(3)若横、纵坐标都是整数的点叫整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,C,B之间的图象E与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
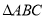 中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以
中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以 cm/s(
cm/s( >0且
>0且 )的速度从C点出发在线段CA上运动,设运动时间为
)的速度从C点出发在线段CA上运动,设运动时间为 秒。
秒。(1)若AB=AC,P在线段BC上,求当
 为何值时,能够使
为何值时,能够使 和
和 全等?
全等?(2)若
 ,求出发几秒后,
,求出发几秒后,  为直角三角形?
为直角三角形?(3)若
 ,当
,当 的度数为多少时,
的度数为多少时,  为等腰三角形?(请直接写出答案,不必写出过程)
为等腰三角形?(请直接写出答案,不必写出过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…依此类推,移动5次后该点对应的数为 , 这样移动10次后该点到原点的距离为a,则|a|= .
相关试题

