【题目】如图,若A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…依此类推,移动5次后该点对应的数为 , 这样移动10次后该点到原点的距离为a,则|a|= . ![]()
参考答案:
【答案】7;14
【解析】解:由题可得,
移动5次后该点对应的数为0+1﹣3+6﹣9+12=7;
移动10次后该点对应的数为0+1﹣3+6﹣9+12﹣15+18﹣21+24﹣27=﹣14,
∴移动10次后该点到原点的距离|a|=14.
故答案分别为7,14.
【考点精析】解答此题的关键在于理解数轴的相关知识,掌握数轴是规定了原点、正方向、单位长度的一条直线,以及对绝对值的理解,了解正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:

(1)求出表中a,b,c的数值,并补全频数分布直方图;
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B,顶点为C,将抛物线在A,C,B之间的部分记为图象E(A,B两点除外).
(1)求抛物线的顶点坐标.
(2)AB=6时,经过点C的直线y=kx+b(k≠0)与图象E有两个交点,结合函数的图象,求k的取值范围.
(3)若横、纵坐标都是整数的点叫整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,C,B之间的图象E与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
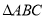 中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以
中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以 cm/s(
cm/s( >0且
>0且 )的速度从C点出发在线段CA上运动,设运动时间为
)的速度从C点出发在线段CA上运动,设运动时间为 秒。
秒。(1)若AB=AC,P在线段BC上,求当
 为何值时,能够使
为何值时,能够使 和
和 全等?
全等?(2)若
 ,求出发几秒后,
,求出发几秒后,  为直角三角形?
为直角三角形?(3)若
 ,当
,当 的度数为多少时,
的度数为多少时,  为等腰三角形?(请直接写出答案,不必写出过程)
为等腰三角形?(请直接写出答案,不必写出过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
①
 (直接开平方法)
(直接开平方法)②
 (用配方法)
(用配方法)③
 (用因式分解法)
(用因式分解法)④

⑤

⑥

⑦

⑧(x-2)(x-5)=-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)6xy2-9x2y-y3; (2)(p-4)(p+1)+3p.
相关试题

