【题目】花香村计划改造一片林地,估计这片林地可种梨树80~133棵.根据经验,若种100棵树,果树成熟后平均每棵树上能结500个梨,在这个基础上每多种一棵梨树,平均每棵会少结3个梨,每少种一棵,平均每棵树会多结4个梨.
(1)如果种植110棵梨树,则总共能结多少个梨?
(2)设种植x棵梨树,总共能结y个梨,
①当80≤x≤100时,求出y与x之间的函数关系式;
②当100<x≤134时,求出y与x之间的函数关系式;
(3)种多少棵梨树,总共能结的梨数最多?最多是多少?
参考答案:
【答案】(1)51700(2)①![]() ②
②![]() (3)当x=133时,有最大值,最大值是53333个梨
(3)当x=133时,有最大值,最大值是53333个梨
【解析】试题分析:(1)、根据题意首先得出每棵树上能结多少果实,然后求出总量;(2)、当80≤x≤100时,平均每棵树上能结[500+4(100-x)]个梨,然后得出函数解析式;当100<x≤120时,平均每棵树上能结[500-3(x-100)]个梨,然后得出函数解析式;(3)、根据两个函数解析式,分别求出每个区间范围内的最大值,最后选择更加大的值得出答案.
试题解析:(1)、如果种110棵树,平均每棵树上能结(500-30)个梨,则总共结51700个梨.
(2)、①、设种植x棵梨树(80≤x≤100),则平均每棵树上能结[500+4(100-x)]个梨,
∴![]() ;
;
②、设种植x棵梨树(100<x≤120),则平均每棵树上能结[500-3(x-100)]个梨,
∴![]() ;
;
(3)、当80≤x≤100时,由于对称轴x=![]() ,所以y随x的增大而增大,
,所以y随x的增大而增大,
故当x=100时,y有最大值,最大值是50000个;
当100<x≤133,![]()
所以当x=133时,有最大值,最大值是53333个梨;
综上所述:当x=133时,有最大值,最大值是53333个梨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产某种产品,每件产品成本是3元,售价是4元,年销售量为10万件,为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x(万元)时,产品的年销售量将是原销售量的y倍,且
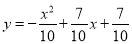 ,如果把利润看作是销售总额减去成本费和广告费,进货都能销售完,试写出年利润S(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大,最大年利润是是多少万元?
,如果把利润看作是销售总额减去成本费和广告费,进货都能销售完,试写出年利润S(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大,最大年利润是是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表
 单位:环
单位:环 :
:第1次
第2次
第3次
第4次
第5次
第6次
甲
10
9
8
8
10
9
乙
10
10
8
10
7
9
根据表格中的数据,可计算出甲、乙两人的平均成绩都是9环.
(1)分别计算甲、乙六次测试成绩的方差;
(2)根据数据分析的知识,你认为选______名队员参赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB=2,C是AB上一点,四边形ACDE和四边形CBFG,都是正方形,设BC=x,
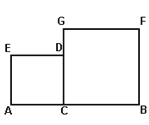
(1)AC=______;
(2)设正方形ACDE和四边形CBFG的总面积为S,用x表示S的函数解析式为S=_____.
(3)总面积S有最大值还是最小值?这个最大值或最小值是多少?
(4)总面积S取最大值或最小值时,点C在AB的什么位置?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在四边形 ABCD 中,∠A=x°,∠C=y°.
(1) ∠ABC+∠ADC= °.(用含 x,y 的代数式表示)
(2) BE、DF 分别为∠ABC、∠ADC 的外角平分线,
①若 BE∥DF,x=30,则 y= ;
②当 y=2x 时,若 BE 与 DF 交于点 P,且∠DPB=20°,求 y 的值.
(3) 如图②,∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,则∠Q= °.(用含 x,y 的代数式表示)
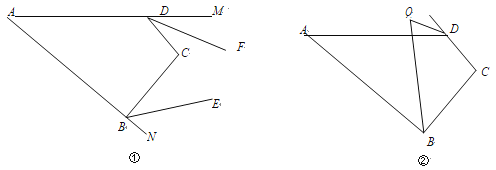
-
科目: 来源: 题型:
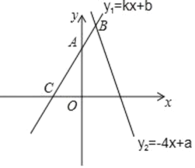
查看答案和解析>>【题目】一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)由图可知,不等式kx+b>0的解集是 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1.
①求点B的坐标;
②求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)
 +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;(2)如果(2+
 )a-(1-
)a-(1- )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
相关试题

