【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
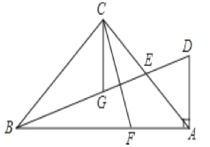
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)利用“ASA”判断△BCG≌△CFA,从而得到BG=CF;
(2)连结AG,利用等腰直角三角形的性质得CG垂直平分AB,则BG=AG,再证明∠D=∠GAD得到AG=DG,所以BG=DG,接着证明△ADE≌△CGE得到DE=GE,则BG=2DE,利用利用△BCG≌△CFA得到CF=BG,于是有CF=2DE;
(3)先得到BG=2,GE=1,则BE=3,设CE=x,则BC=AC=2CE=2x,在Rt△BCE中利用勾股定理得到x![]() +(2x)
+(2x)![]() =3
=3![]() ,解得x=
,解得x=![]() ,所以BC=
,所以BC=![]() ,AB=
,AB=![]() BC=
BC=![]() ,然后在Rt△ABD中利用勾股定理计算AD的长.
,然后在Rt△ABD中利用勾股定理计算AD的长.
(1)证明:∵∠ACB=90°,AC=BC,
∴△ACB为等腰直角三角形,
∴∠CAF=∠ACG=45°,
∵CG平分∠ACB,
∴∠BCG=45°,
在△BCG和△CFA中
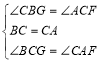 ,
,
∴△BCG≌△CFA,
∴BG=CF;
(2)证明:连结AG,
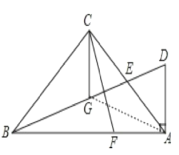
∵CG为等腰直角三角形ACB的顶角的平分线,
∴CG垂直平分AB,
∴BG=AG,
∴∠GBA=∠GAB,
∵AD⊥AB,
∴∠D+∠DBA=90°,∠GAD+∠GAB=90°,
∴∠D=∠GAD,
∴AG=DG,
∴BG=DG,
∵CG⊥AB,DA⊥AB,
∴CG∥AD,
∴∠DAE=∠GCE,
∵E为AC边的中点,
∴AE=CE,
在△ADE和△CGE中
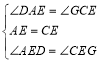 ,
,
∴△ADE≌△CGE,
∴DE=GE,
∴DG=2DE,
∴BG=2DE,
∵△BCG≌△CFA,
∴CF=BG,
∴CF=2DE;
(3)∵DE=1,
∴BG=2,GE=1,即BE=3,
设CE=x,则BC=AC=2CE=2x,
在Rt△BCE中,x![]() +(2x)
+(2x) ![]() =3
=3![]() ,解得x=
,解得x=![]() ,
,
∴BC=![]() ,
,
∴AB=![]() BC=
BC=![]() ,
,
在Rt△ABD中,∵BD=4,AB=![]() ,
,
∴AD=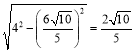 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AC和BC在同一直线上,AC=8cm,BC=3cm,则线段AC的中点和BC中点之间的距离是( )
A.5.5cmB.2.5cm
C.4cmD.5.5cm或2.5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°.∠BOC=30°,OM平分∠AOC,ON平分∠BOC.

(1)求∠MON的度数;
(2)若∠BOC=60°,其他条件不变,则∠MON= ;
(3)若∠AOB=α,其他条件不变,求∠MON的度数;
(4)从上面的结果能看出什么规律?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|

(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③代数式|x+1|+|x﹣2|取最小值时,相应的整数x的取值是 .
-
科目: 来源: 题型:
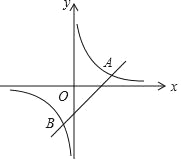
查看答案和解析>>【题目】如图,已知一次函数y=x﹣2与反比例函数y=
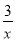 的图象交于A、B两点.
的图象交于A、B两点.(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=
 x3与反比例函数y=
x3与反比例函数y= 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为___,k的值为___;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y=
 的图象,当y2时,请直接写出自变量x的取值范围。
的图象,当y2时,请直接写出自变量x的取值范围。
相关试题

