【题目】(1)阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|

(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③代数式|x+1|+|x﹣2|取最小值时,相应的整数x的取值是 .
参考答案:
【答案】(2)①3,3,4;②|x+1|,1或﹣3;③﹣1、0、1、2.
【解析】
根据两点之间的距离是哪些线段的和差以及绝对值的性质即可得到两点之间的距离公式,根据到两点的距离之和最小时这个点应该在已知的两点所确定的线段上
解:(2)①5-2=3,-2-(-5)=3,1-(-3)=4
②数轴上表示x和﹣1的两点A和B之间的距离是![]()
∵|x+1|=2,
∴x+1=±2,
∴x=1或﹣3,
(3)由题意可知:|x+1|+|x﹣2|表示数x到﹣1和2之间的距离之和,
∴当﹣1≤x≤2时,
|x+1|+|x﹣2|可取得最小值,
∴x的整数为﹣1,0,1,2;
故答案为:
(1)3;3;4
(2)|x+1|;1或﹣3
(3)﹣1,0,1,2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20
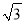 m,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45°,求AF的长度.
m,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45°,求AF的长度.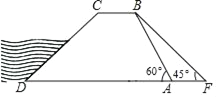
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AC和BC在同一直线上,AC=8cm,BC=3cm,则线段AC的中点和BC中点之间的距离是( )
A.5.5cmB.2.5cm
C.4cmD.5.5cm或2.5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°.∠BOC=30°,OM平分∠AOC,ON平分∠BOC.

(1)求∠MON的度数;
(2)若∠BOC=60°,其他条件不变,则∠MON= ;
(3)若∠AOB=α,其他条件不变,求∠MON的度数;
(4)从上面的结果能看出什么规律?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
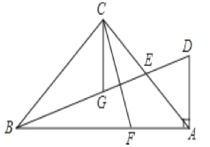
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=x﹣2与反比例函数y=
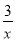 的图象交于A、B两点.
的图象交于A、B两点.(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
相关试题

