搜索
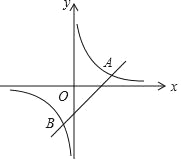
【题目】如图，已知一次函数y=x﹣2与反比例函数y=
的图象交于A、B两点．
（1）求A、B两点的坐标；
（2）观察图象，直接写出一次函数值小于反比例函数值的x的取值范围；
（3）坐标原点为O，求△AOB的面积．
参考答案：
【答案】（1）A（3，1）、B（﹣1，﹣3）（2）x＜﹣1或0＜x＜3（3）4
【解析】试题分析：（1）联立方程组，解方程组即可得到A、B的坐标；
（2）根据图像确定一次函数的图像在反比例函数的图像上的x范围即可；
（3）过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，构造三角形，求三角形的面积和即可.
试题解析：（1）联立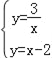
解得：
或
∴A（3，1）、B（﹣1，﹣3）
（2）x的取值范围为：x＜﹣1或0＜x＜3
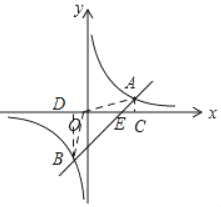
（3）过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，
令y=0代入y=x﹣2
∴x=2，
∴E（2，0）
∴OE=2
∵A（3，1）、B（﹣1，﹣3）
∴AC=1，BD=3，
∴△AOE的面积为：
ACOE=1，
△BOE的面积为： BDOE=3，
∴△ABC的面积为：1+3=4，
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠AOB＝90°．∠BOC＝30°，OM平分∠AOC，ON平分∠BOC．
（1）求∠MON的度数；
（2）若∠BOC＝60°，其他条件不变，则∠MON＝ ；
（3）若∠AOB＝α，其他条件不变，求∠MON的度数；
（4）从上面的结果能看出什么规律？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）阅读下面材料：
点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|＝|OB|＝|b|＝|a﹣b|；当A、B两点都不在原点时，
①如图2，点A、B都在原点的右边|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝b﹣a＝|a﹣b|；
②如图3，点A、B都在原点的左边，|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝﹣b﹣（﹣a）＝|a﹣b|；
③如图4，点A、B在原点的两边，|AB|＝|OB|+|OA|＝|a|+|b|＝a+（﹣b）＝|a﹣b|
（2）回答下列问题：
①数轴上表示2和5的两点之间的距离是 ，数轴上表示﹣2和﹣5的两点之间的距离是 ，数轴上表示1和﹣3的两点之间的距离是 ；
②数轴上表示x和﹣1的两点A和B之间的距离是 ，如果|AB|＝2，那么x为 ；
③代数式|x+1|+|x﹣2|取最小值时，相应的整数x的取值是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°，AC=BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点D，CG平分∠ACB交BD于点G.F为AB边上一点，连接CF，且∠ACF=∠CBG.
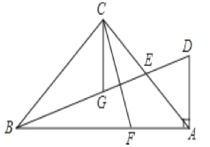
(1)求证：BG=CF；
(2)求证：CF=2DE；
(3)若DE=1，求AD的长
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回），商场根据两小球所标金额的和返还相应价格购物券,可以重新在本商场消费，某顾客刚好消费200元．
（1）该顾客至少可得到_____元购物券，至多可得到_______元购物券；
（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,已知一次函数y=
x3与反比例函数y=
的图象相交于点A(4,n)，与x轴相交于点B.
(1)填空：n的值为___，k的值为___；
(2)以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；
(3)观察反比例函数y=
的图象，当y2时，请直接写出自变量x的取值范围。 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，在数轴上有A，B两点，所表示的数分别为-10，4，点A以每秒5个单位长度的速度向右运动，同时点B以每秒3个单位长度的速度也向左运动，如果设运动时间为t秒，解答下列问题：
（1）运动前线段AB的长为 ； 运动1秒后线段AB的长为 ；
（2）运动t秒后，点A，点B运动的距离分别为 ；用t表示A，B分别为 ．
（3）求t为何值时，点A与点B恰好重合；
（4）在上述运动的过程中，是否存在某一时刻t，使得线段AB的长为6，若存在，求t的值； 若不存在，请说明理由．
相关试题
