搜索
【题目】已知线段AC和BC在同一直线上，AC＝8cm，BC＝3cm，则线段AC的中点和BC中点之间的距离是（ ）
A.5.5cmB.2.5cm
C.4cmD.5.5cm或2.5cm
参考答案：
【答案】D
【解析】
先根据线段中点的定义求出CE，CF，然后分点B不在线段AC上时，EF＝CE+CF，点B在线段AC上时，EF＝CE﹣CF两种情况计算即可得解．
解：设AC、BC的中点分别为E、F，
∵AC＝8cm，BC＝3cm，
∴CE＝
AC＝4cm，CF＝BC＝1.5cm，
如图所示，当点B不在线段AC上时，EF＝CE+CF，
＝4+1.5，
＝5.5cm，
如图所示，当点B在线段AC上时，EF＝CE﹣CF，
＝4﹣1.5，
＝2.5cm，
综上所述，AC和BC中点间的距离为2.5cm或5.5cm．
故答案为：2.5cm或5.5cm
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图,一次函数y=kx+3的图象与反比例函数y=
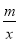(x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B. 一次函数的图象分别交x轴、y轴于点C. 点D,且S△DBP=27,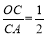
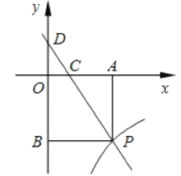
(1)求点D的坐标；
(2)求一次函数与反比例函数的解析式
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线l1∥l2，⊙O与l1和l2分别相切于点A和点B，点M和点N分别是l1和l2上的动点，MN沿l1和l2平移，若⊙O的半径为1，∠1=60°，下列结论错误的是（ ）
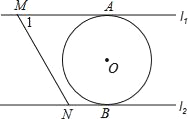
A. MN=
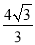B. 若MN与⊙O相切，则AM=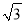
C. l1和l2的距离为2 D. 若∠MON=90°，则MN与⊙O相切
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，水坝的横断面是梯形，背水坡AB的坡角∠BAD=60°，坡长AB=20
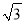m，为加强水坝强度，将坝底从A处向后水平延伸到F处，使新的背水坡的坡角∠F=45°，求AF的长度．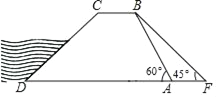
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠AOB＝90°．∠BOC＝30°，OM平分∠AOC，ON平分∠BOC．
（1）求∠MON的度数；
（2）若∠BOC＝60°，其他条件不变，则∠MON＝ ；
（3）若∠AOB＝α，其他条件不变，求∠MON的度数；
（4）从上面的结果能看出什么规律？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）阅读下面材料：
点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|＝|OB|＝|b|＝|a﹣b|；当A、B两点都不在原点时，
①如图2，点A、B都在原点的右边|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝b﹣a＝|a﹣b|；
②如图3，点A、B都在原点的左边，|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝﹣b﹣（﹣a）＝|a﹣b|；
③如图4，点A、B在原点的两边，|AB|＝|OB|+|OA|＝|a|+|b|＝a+（﹣b）＝|a﹣b|
（2）回答下列问题：
①数轴上表示2和5的两点之间的距离是 ，数轴上表示﹣2和﹣5的两点之间的距离是 ，数轴上表示1和﹣3的两点之间的距离是 ；
②数轴上表示x和﹣1的两点A和B之间的距离是 ，如果|AB|＝2，那么x为 ；
③代数式|x+1|+|x﹣2|取最小值时，相应的整数x的取值是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°，AC=BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点D，CG平分∠ACB交BD于点G.F为AB边上一点，连接CF，且∠ACF=∠CBG.
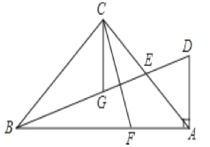
(1)求证：BG=CF；
(2)求证：CF=2DE；
(3)若DE=1，求AD的长
相关试题
